Convex Optimization 02

Coursera 2018.03

Convex sets

1. Affine and convex set

• affine set

  

  • affine set中的点都可以表示为其他两个不同的点的组合，注意这里的点并不局限于二维平面上的点。
    没有限制$\theta \ge 0$。

• convex set

  

• convex combination and convex hull

  

• convex cone

  

2. Examples

• hyperplane and halfspaces

  

  • 向量内积的意义

    $$\frac{a^Tb}{\parallel b \parallel}$$
    $a$在$b$上的投影距离。

    

    $$\frac{a^Tb}{\parallel a \parallel \parallel b \parallel} = \parallel a \parallel \parallel b \parallel \cos \theta$$
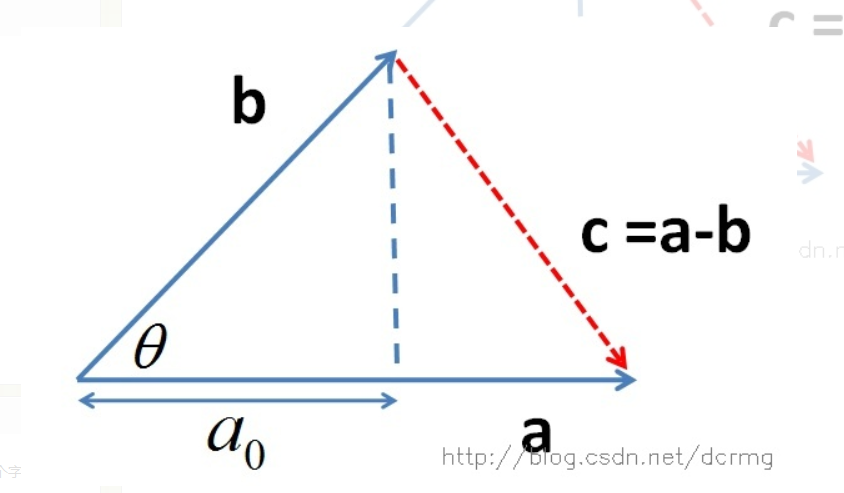
    证明如图，使用余弦定理。

• euclidean ball and ellipsoid

  

  • 对称正定矩阵$P$是unique的

    by the way, this representation here, is unique, in other words, if this is equal to another set with a different. With another p. Those two matrices have to be equal and I'm assuming that they're symmetric, here, right? If they're not symmetric that's false. but if they're, if they're symmetric which you can assume without loss of generality, then it's true.

  • $A$并不是unique的，例如$A=Q,Q^TQ=I$

    here the A in this representation is not unique. A is, A there's multiple A's here that would give you the same Set in particular if I take A and I multiply it on the right by Q, here where Q is an orthogonal matrix. So Q trans, Q is square and satisfies
    that. Then for sure AQ can be substituted for A here and you get the same set. And the reason is actually quite simple. the reason is if I take a something whose norm is less than 1 and I multiple it by an orthongonal vector I get something whose norm is less than 1 and in fact it goes vice versa so that's why it's the same thing.

• norm ball and norm cones

  

• polyhedra

  

  And another name for this is polytope, is that a name. And, so, and then what gets even more bizarre, is some people refer. Distinguish between a polytope and a polyhedron by, using one to refer to the bounded version. So if it's a bounded polyhedron it's called a polytope and then believe it or not, you can find another author who exactly switches these, right? So, for example, the general is a polytope and a bounded one is a polyhedron.

• positive semidefinite cone

  

  注意此处符号表示的是正定与否，并不element-wise的大于小于。

3. Operations that preserve convexity

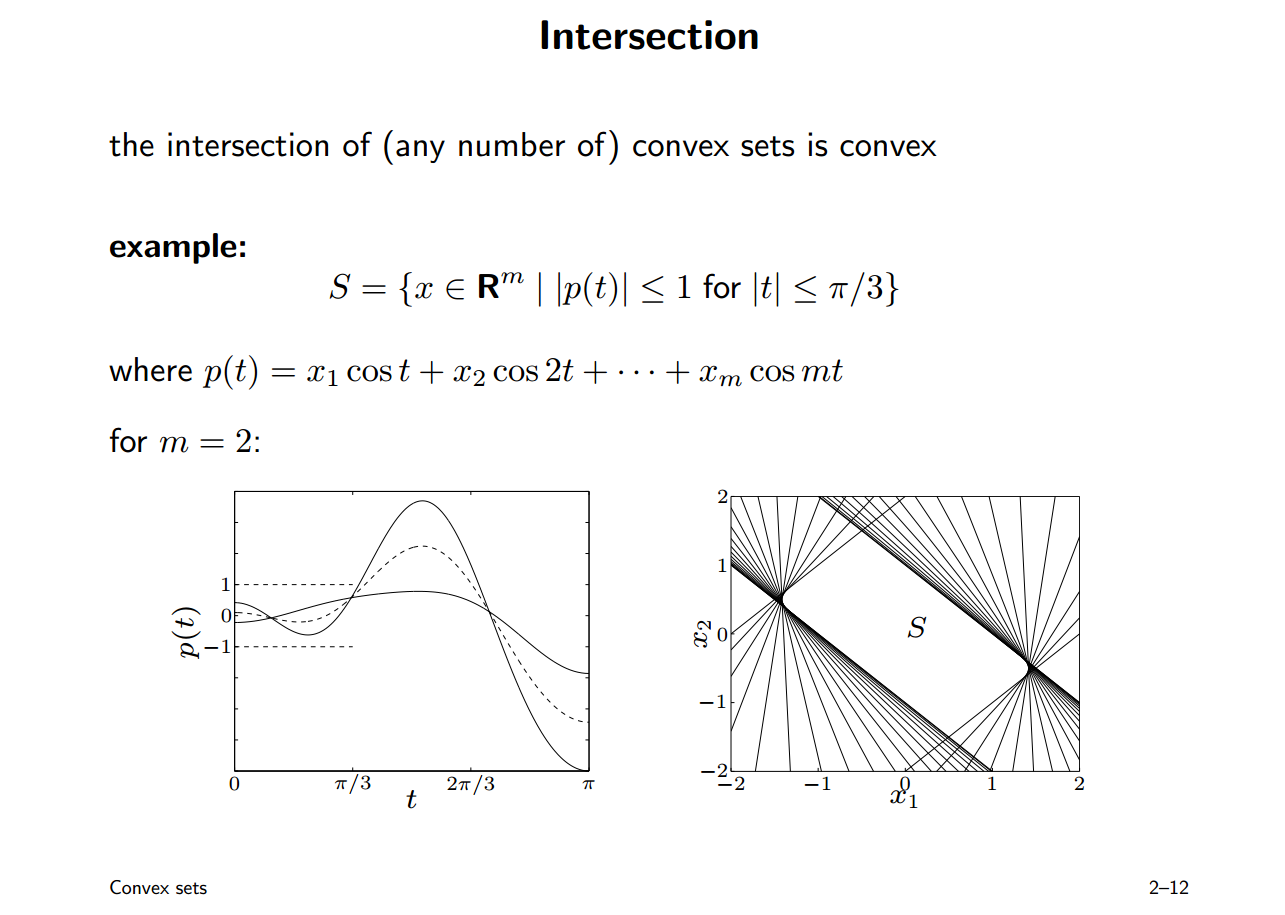
• intersection

  

  

• Affine function

  

  • Affine function的image是convex

    Affine function的inverse image也是convex的

  • 这个matrix inequality没看懂

• perspective function and linear-fractional function

  

  

  scp -r zhaoshuai@10.76.1.49:/home/zhaoshuai/pyenv35/SEE/chainer/train_centered_modified train_centered_modified

4. Generalized inequalities

• generalized inequalities

  

  

  

  • minimum是unique的

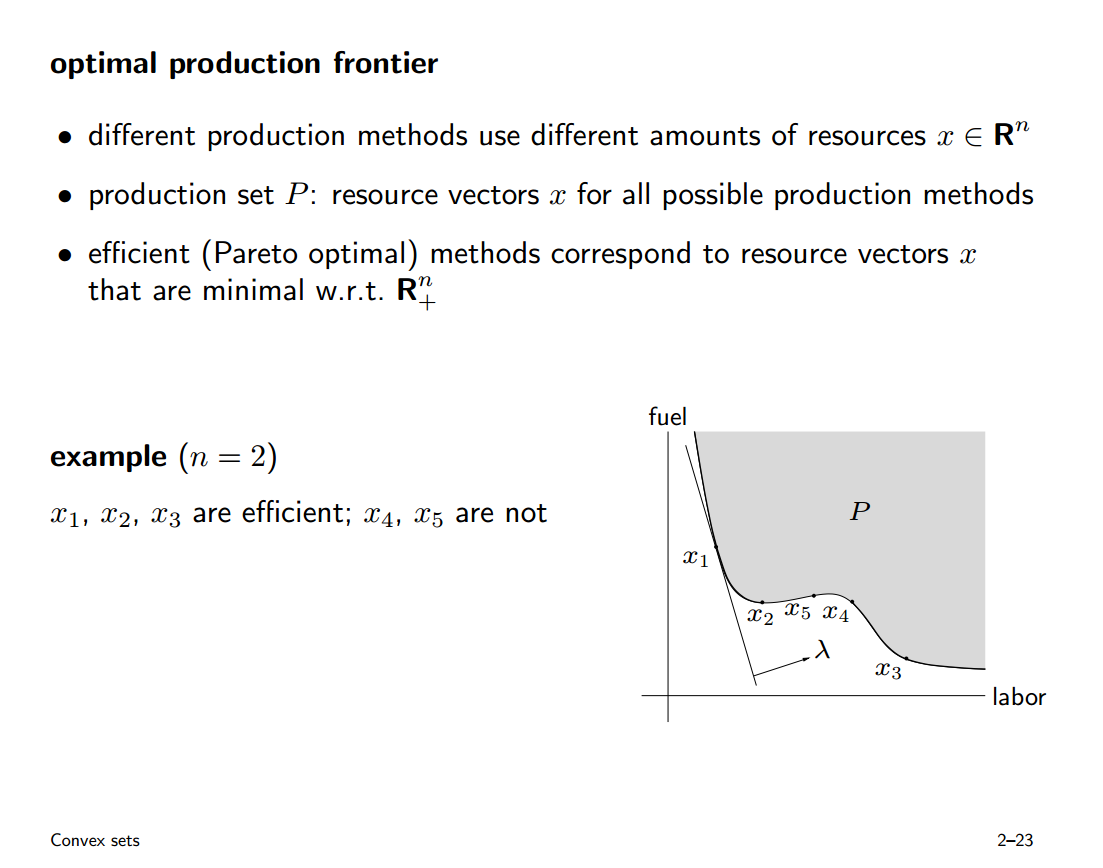
    minimal element指的是，集合中比它小的就只有它自身。注意象限的使用，比$x_2$小的都在第三象限，第二、第四象限不可以比较。注意这里所说的大小的定义。

5. Separating hyperplane and supporting hyperplane

• Separating hyperplane theorem

  

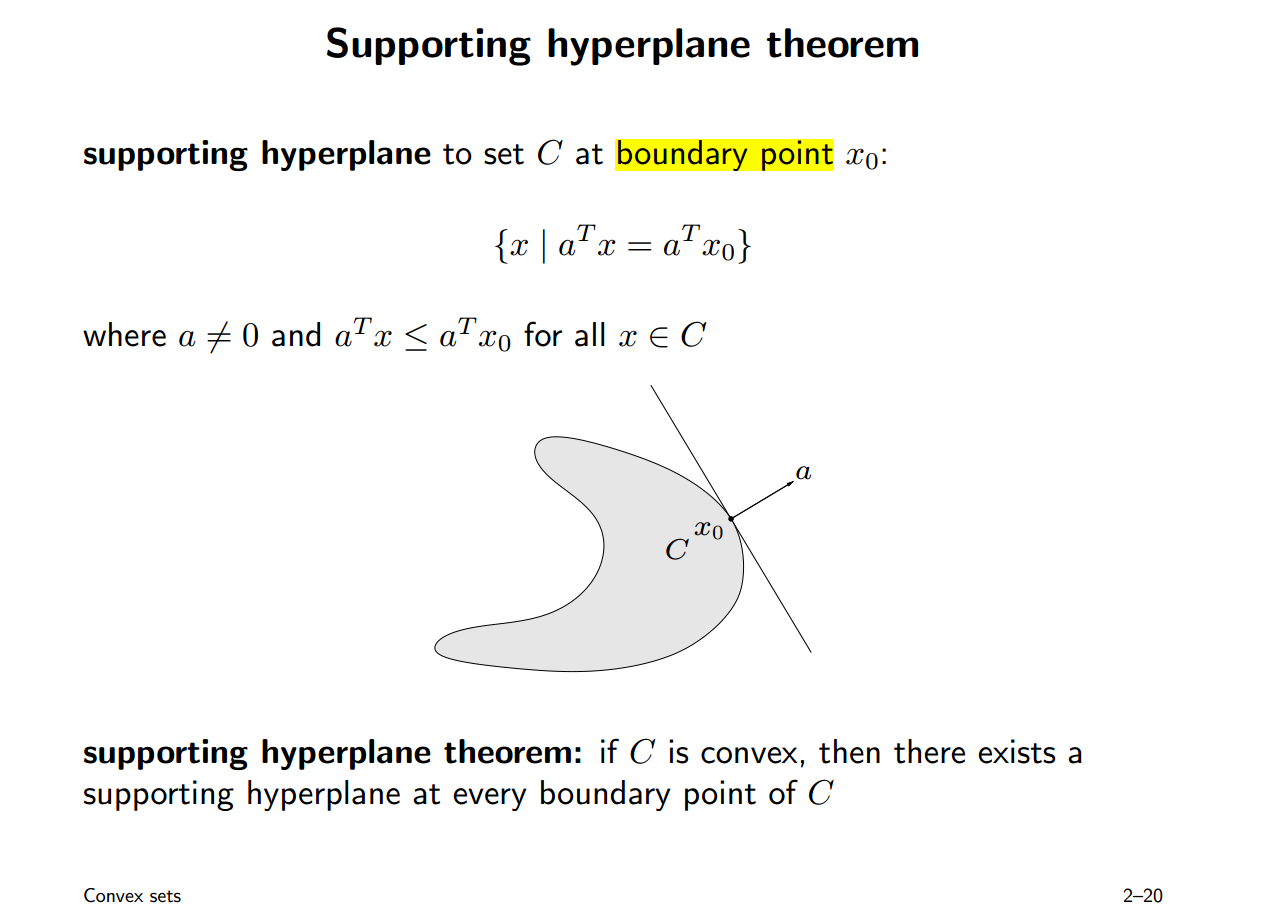
• Supporting hyperplane theorem

  

6. Dual cones and generalized inequalities