@floatsd
2016-04-12T13:12:31.000000Z
字数 4353
阅读 1437
聚类算法实验报告
人工智能导论实验报告
1.K-means
1.1实验原理
- 已知观测集,其中每个观测都是一个维实矢量,k-平均聚类要把这n个观测划分到个集合中,使得组内平方和最小。换句话说,它的目标是找到使得满足下式,其中是中所有点的均值。
- k-平均聚类的目的是:把n个点划分到k个聚类中,使得每个点都属于离他最近的均值(此即聚类中心)对应的聚类,以之作为聚类的标准。
- 首先设定已知初始的k个均值点,算法的按照下面两个步骤交替进行 :
- 1.分配:将每个观测分配到聚类中,使得组内平方和达到最小。因为这一平方和就是平方后的欧氏距离,所以很直观地把观测分配到离它最近得均值点即可,其中每个都只被分配到一个确定的聚类中,尽管在理论上它可能被分配到2个或者更多的聚类。
- 2.更新:计算得到上步得到聚类中每一聚类观测值的图心,作为新的均值点。此处取值有很多不同的方法,如直接平均坐标、取中值、取均值、或欧式距离等。
- 1.分配:将每个观测分配到聚类中,使得组内平方和达到最小。因为这一平方和就是平方后的欧氏距离,所以很直观地把观测分配到离它最近得均值点即可,其中每个都只被分配到一个确定的聚类中,尽管在理论上它可能被分配到2个或者更多的聚类。
- 交替步骤一和步骤二,这一算法将在对于观测的分配不再变化时收敛。由于交替进行的两个步骤都会减小目标函数的值,并且分配方案只有有限种,所以算法一定会收敛于某一(局部)最优解,此时均值点的位置变化小于一定阈值,算法停止。
- 有一个需要注意的是在算法开始时种子点的选取。通常使用的初始化方法有Forgy方法和随机划分方法。Forgy方法随机地从数据集中选择k个观测作为初始的均值点;而随机划分方法则随机地为每一观测指定聚类,然后运行“更新”步骤,即计算随机分配的各聚类的图心,作为初始的均值点。Forgy方法易于使得初始均值点散开,随机划分方法则把均值点都放到靠近数据集中心的地方。
- 实验中使用的是Forgy方法。
1.2实验结果
- 模拟数据两组共450个:
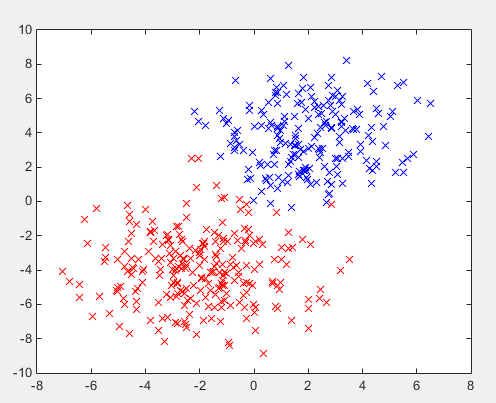
- 取k为3,得到结果如下图:
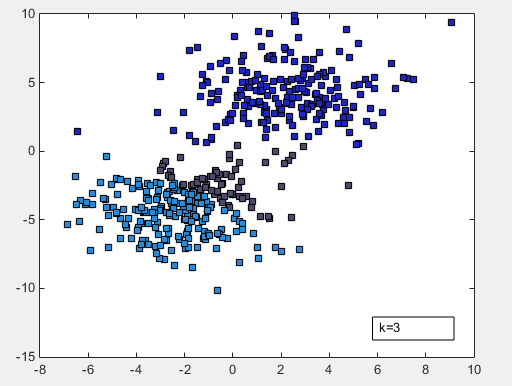
- 取k为4,得到结果如下图:
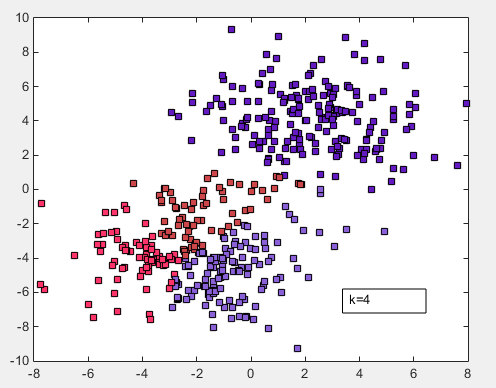
- 文件有两个,一为生成模拟数据,二为k-means算法,每次运行模拟数据脚本会重新生成数据,每次运行k-means算法脚本会重新选点,所以每张图中点不一样。
1.3源代码
1.3.1 数据模拟
clc;clear all;close all;%生成data1;num_data1=200;data1.feature(:,1)=2*randn(num_data1,1)+2;data1.feature(:,2)=2*randn(num_data1,1)+4;%生成data2;num_data2=250;data2.feature(:,1)=2*randn(num_data2,1)-2;data2.feature(:,2)=2*randn(num_data2,1)-4;plot(data1.feature(:,1),data1.feature(:,2),'bx');hold on;plot(data2.feature(:,1),data2.feature(:,2),'rx');%合并data,数据存储在data.feature矩阵一二列data.type=[ones([num_data1 1]);2*ones([num_data2 1])];data.feature=[data1.feature;data2.feature];
1.3.2 寻找图心
function [ output ] = f_med( pos,label,cluster )% 使用均值计算中心要素% 输入点的位置矩阵(x,y),当前标签% 输出新中心点并更新标签n=length(pos);A=pos(1,:);for i=2:n%获取当前标签所有点if(label(i)==cluster)A=[A;pos(i,:)];endend%分别取聚类坐标均值v_medx=mean(A(:,1));v_medy=mean(A(:,2));output=[v_medx v_medy];end
1.3.3 K-means
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%n=length(data.feature); %得到数据个数%在数据中随机初始化种子num_seed个;%并获取对应数据feature值num_seed=4;seed(:,1)=randi(n,num_seed,1);for i=1:num_seedseed(i,2:3)=data.feature(seed(i,1),:);enddis=zeros([1 num_seed]);nucleus=zeros([num_seed 2]);diff=zeros([1 num_seed]);%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%k_Meansplot(0,0);hold on;for k=1:nfor i=1:nfor j=1:num_seeddis(j)=(data.feature(i,1)-seed(j,2))^2+...(data.feature(i,2)-seed(j,3))^2; %当前数据到各中心距离end[m0,n0]=find(dis==min(min(dis))); %得到最小距离是哪个并分配data.label(i,1)=n0;end%更新中心要素,函数f_med计算一个类群的坐标均值。for j=1:num_seednucleus(j,:)=f_med(data.feature,data.label,j);diff(j)=sqrt((nucleus(j,1)-seed(j,2))^2)+sqrt((nucleus(j,2)-seed(j,3))^2);end%验证中心变化量;%当中心变化小于一定值得到局部最优解,跳出循环;if sqrt(sum(diff))>3for j=1:num_seedseed(j,1)=nucleus(j,1);plot(seed(j,2),seed(j,3),'g*');hold on;endelsebreak;endend%绘制结果for i=1:nfor j=1:num_seedif(data.label(i,1)==j)plot(data.feature(i,1),data.feature(i,2),...'ks','MarkerFaceColor',...[abs(cos(j^6)) abs(0.7*cos(j^3)) abs(sin(j^2))]);endendend
2.Hierarchical Clustering
2.1 实验原理
和k-means不同,层次聚类(Hierarchical Clustering)一开始不需要知道样本待聚类数目,假设有N个待聚类的样本,基本步骤为:
- 初始化每个样本归为一类,计算每两个类之间的距离,也就是样本与样本之间的相似度;
- 寻找各个类之间最近的两个类,把他们归为一类;
- 重新计算新生成的这个类与各个旧类之间的相似度;
- 重复2和3直到剩下的类的相似度都小于一阈值,结束循环。
其中相似度的计算方法有许多种,举例如下:
| 方法 | 公式 |
|---|---|
| 欧氏距离 | |
| 欧氏距离的平方 | |
| 曼哈顿距离 | |
| 最大距离 |
2.2 实验结果
- 分类结果如下;
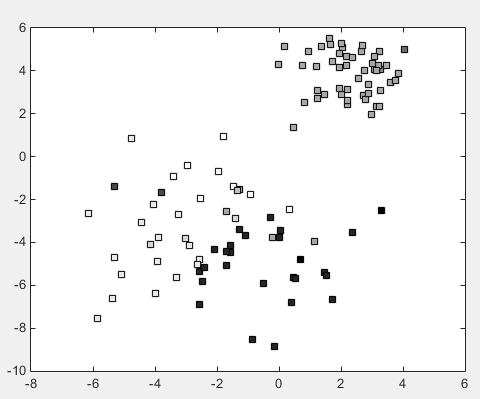
- 设定阈值为0.95倍最大值情况,最后归并剩下了12类,以下是层次聚类归并的标签值:
2.3 实验代码
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%使用欧式距离计算dis=ones([n n]);min_v=0;for k=1:inffor i=1:nfor j=1:n%计算类与类间相似度diffx=data.feature(i,1)-data.feature(j,1);diffy=data.feature(i,2)-data.feature(j,2);dis(i,j)=sqrt(diffx^2+diffy^2);if(dis(i,j)<=min_v)dis(i,j)=max(max(dis));endendend%函数f_min获得矩阵最小值的行列坐标和值%获取相似度矩阵的最大值(距离最短)[min_row,min_col,min_v]=f_min(dis);%得到相似度最大两类归并data.Label(min_row,1)=min_col;%阈值设定if(min_v>0.98*max(max(dis)))break;endend%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%查看剩余标签值counter=zeros([n 1])for i=1:ncounter(data.Label(i,1),1)=counter(data.Label(i,1),1)+1;enda=find(counter);
3.算法比较
本次实验测试了最基本的k-means算法和层次算法聚类,其中k-means图心选取直接取的坐标均值,层次算法相似度使用欧氏距离,可以调节k-means初始点个数和层次算法的阈值。
- 效率上来看,k-means算法要远远快于层次算法,层次算法的数据量已经缩减到了100但还是很慢;
- k-means的初始值是人为给定的,要在一开始就知道总共有几个类,然而我们得到的数据经常并不知道应该分几类,层次算法就没有这个问题;
- k-means算法每次初始化的选点是不同的,得出来的结果也会差很多,聚类效果时好时坏,层次算法对于同个样本得出的结果是一样的;
- 数据给了线性不可分的形式,光是肉眼看着就觉得惨不忍睹,没有测试准确率。
