实验七 DSP算法实验——快速傅里叶变换（FFT）算法

note_DSP

1 实验目的

• 掌握用窗函数法设计FFT快速傅里叶的原理和方法
• 熟悉FFT快速傅里叶特性
• 了解各种窗函数对快速傅里叶特性的影响

2 实验原理

• 快速傅里叶变换（英语：Fast Fourier Transform, FFT），是计算序列的离散傅里叶变换（DFT）或其逆变换的一种算法。傅里叶分析将信号从原始域（通常是时间或空间）转换到频域的表示或者逆过来转换。FFT会通过把DFT矩阵分解为稀疏（大多为零）因子之积来快速计算此类变换。因此，它能够将计算DFT的复杂度从只用DFT定义计算需要的 $O(n^{2})$，降低到$O(n\log n)$（比如$2^3$个点只要三次计算），其中$n$为数据大小。
• 公式的推导和演算比较复杂，下面用蝶形图的方式来直观表达FFT，实验中是将时域信号转换为频域信号，则图中取8点的时域到频域的快速傅里叶变换蝶形图为例。
  
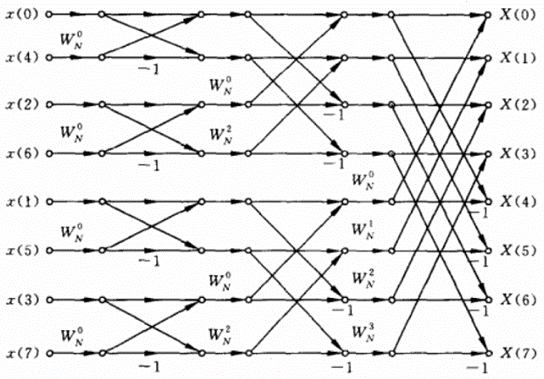
• 图中的参数$W_n$为旋转因子，左侧$x(i)$为时域信号，右侧$X(k)$为频域信号，对应FFT参数生成公式为，可以看做“奇数项”和“偶数项”的和。
  $$X(k)=\sum_{r=0}^{\frac{N}{2}-1}x_1W^{rk}_{\frac{N}{2}}+W^{K}_{N}\sum_{r=0}^{\frac{N}{2}-1}x_2W^{rk}_{\frac{N}{2}}=X_1(k)+W^{k}_{N}X_2(k)$$
• 这里的旋转因子其实是来自DFT定义（离散化的傅里叶变换）：
  $${\displaystyle X_{k}=\sum _{n=0}^{N-1}x_{n}e^{-{i2\pi k{\frac {n}{N}}}}\qquad k=0,\dots ,N-1.}$$
• 而旋转因子$W_n$其实就是$e^{-{j\frac{2\pi}{N}}}$的表示，且易得${W_n}^{kN}=e^{-{j2\pi}k}=1$
• 编程实现的以正弦波为例的实验流程图如下：
  

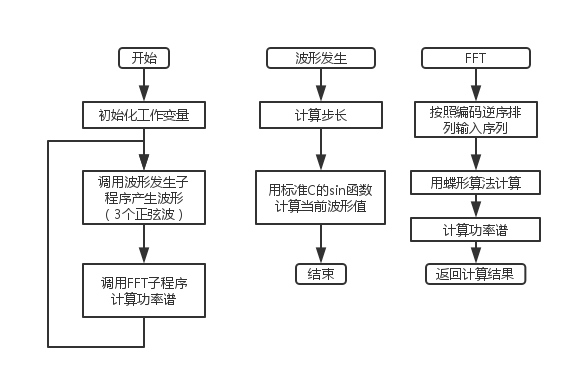
3 实验内容

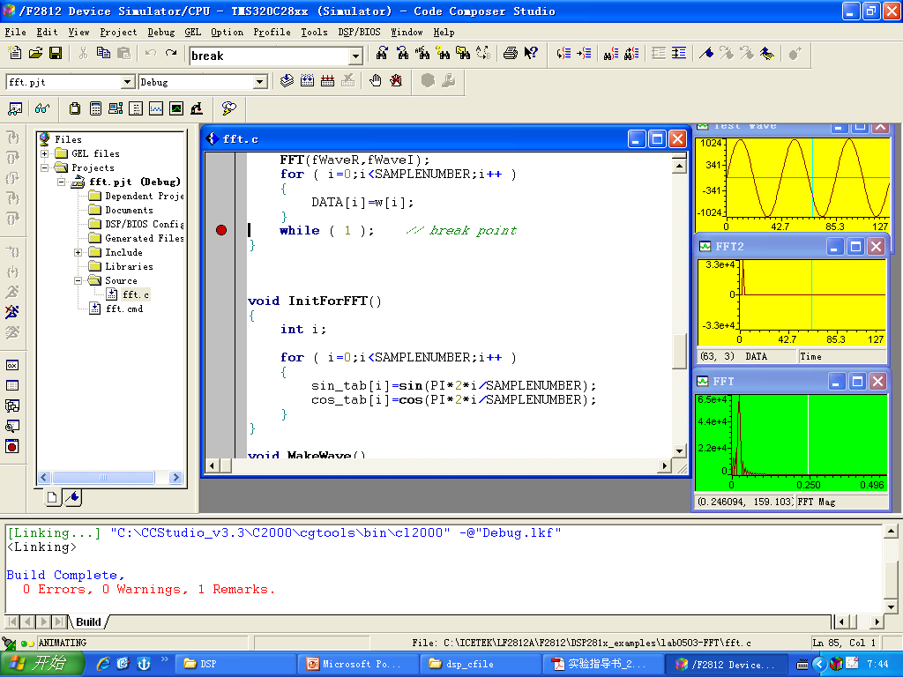
• 在仿真环境下打开FFT.pjt，编译下载程序，设置观察窗口分别观察时域波形，实际功率谱和FFT计算结果如下图，可以看到功率谱和FFT计算结果相近：
  
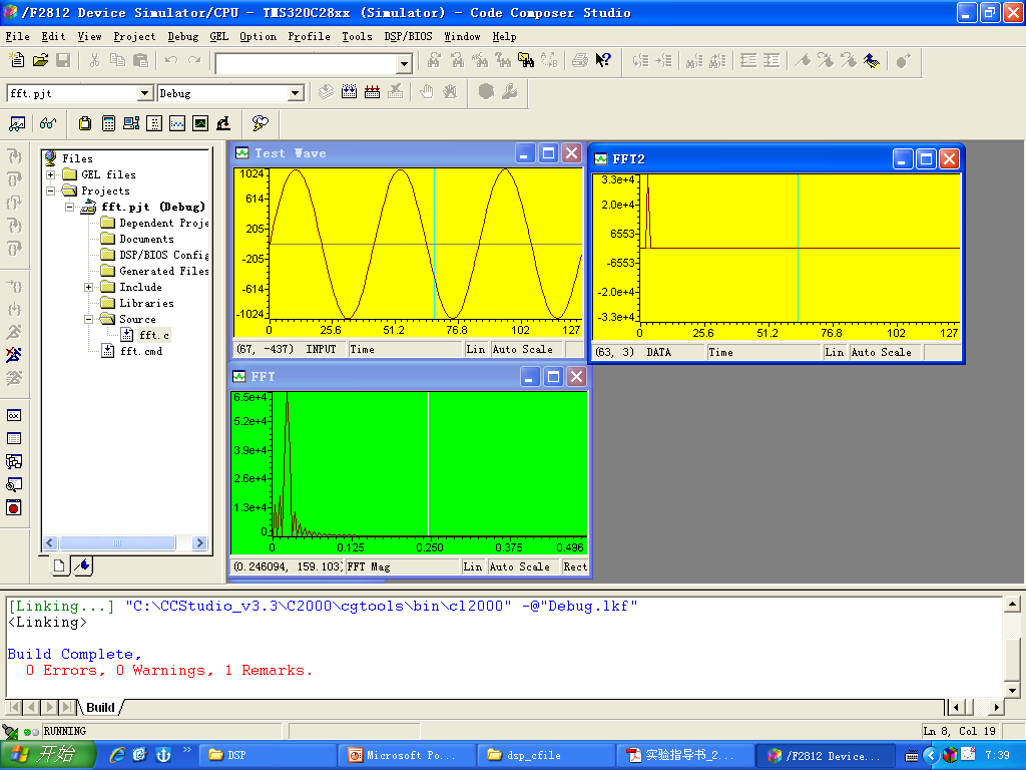
• 在循环里设置断点如下：
  

4 实验结论

• 第二节提到过，FFT把N点DFT分解为几个较短的DFT，可使乘法次数大大减少，且旋转因子具有周期性和对称性，在编程实现上也有极大的优势。
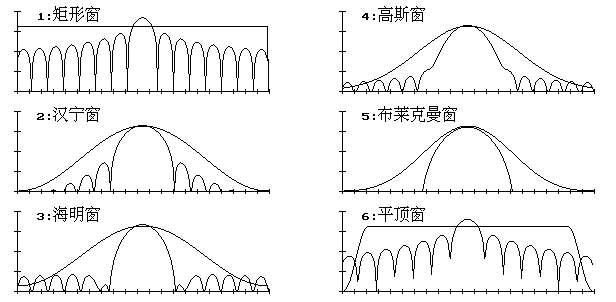
• 下面来看窗函数，窗函数可以想象实在频域里加窗对信号进行过滤。可以利用窗函数设计高通、低通、带限等滤波器，不同的窗函数对不同类型的信号有不同的适应性。