对流扩散问题的离散：中心差分，迎风格式，混合格式和power-law格式

FVM

---

本文是An Introduction to computational fluid dynamics The Finite Volume Method Ch 5 的学习笔记

序言

对流扩散问题要处理的是同时包含对流项和扩散项的微分方程，形如下式：

$$\begin{equation} \mathrm{div}(\rho \boldsymbol{u}\phi) = \mathrm{div}(\Gamma \mathrm{grad} \phi) + S_{\phi} \end{equation}$$

其中左侧即是对流项，$\mathrm{div}$代表通量；右侧第一项是扩散项，其通量（$\mathrm{div}$）是梯度的函数（$\mathrm{grad}$）。

对这一方程，我们同样在控制体上积分，使用高斯定理就可以将其转化为代数方程。接下来以一个一维对流扩散问题为例说明离散和求解的基本过程。其中我们使用中心差分格式离散所有需要离散的项，这是出于简单和直观的考虑。

一维对流扩散问题的中心差分解法

中心差分格式的实现

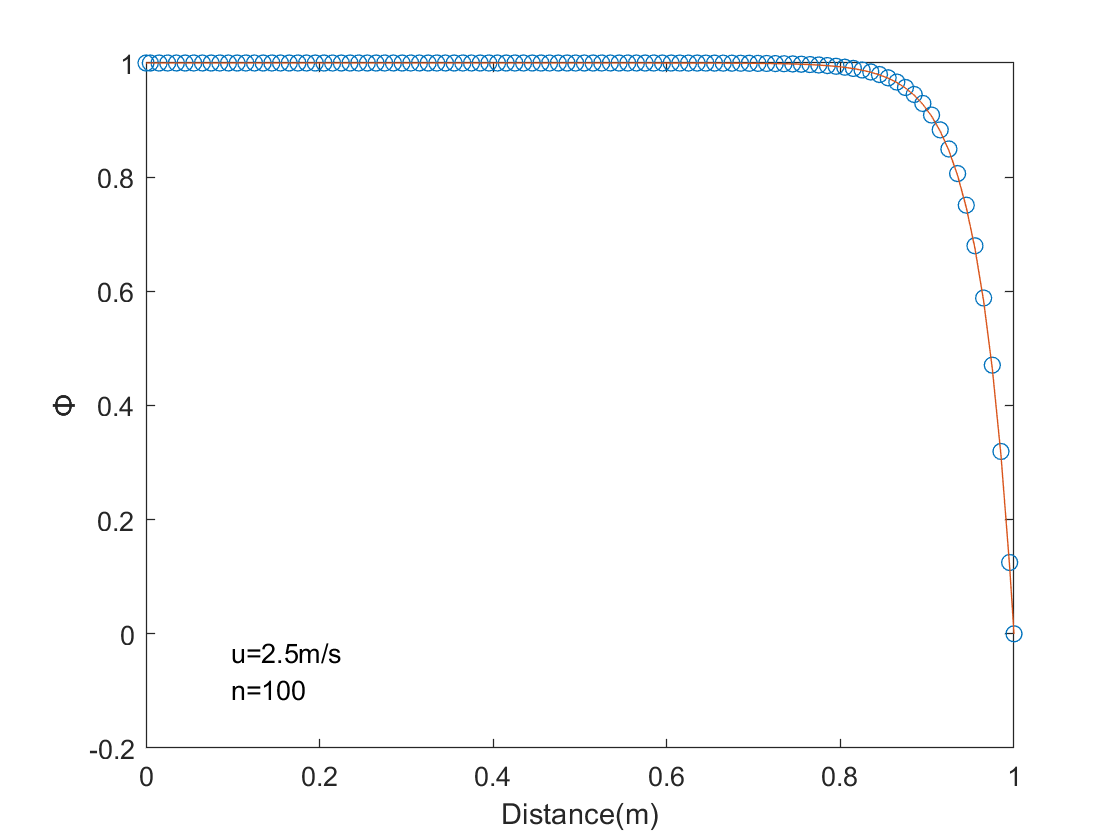
Figure 1.解析解与数值解对比，节点数为100

离散格式的性质以及中心差分格式的评估

推导和使用离散格式时需要考察的特性主要有三种：

*守恒性（Conservativeness）
*有界性（Boundedness）
*传输性（Transportiveness）

守恒性

守恒性被满足的核心在于，从一侧穿过一个控制面的通量用与从另一侧穿出来的通量相等。数学上，为了满足这一条件，在一个面两侧节点的通量表达式应相同。
作为例子，我们考虑一维扩散问题中相邻的两个不是边界的节点。假定西侧的叫做节点2，东侧的叫做节点3。那么根据中心差分格式，从西向东穿过控制面的通量是：

$$\begin{equation} \Gamma_{e2}\frac{\phi_3 - \phi_2}{\delta x} \end{equation}$$
而从东向西穿过控制面的通量是：
$$\begin{equation} \Gamma_{w3}\frac{\phi_3 - \phi_2}{\delta x} \end{equation}$$
显然当两边的传输系数相同时，二者形式完全相同，因此不会有守恒性的问题。其他的离散格式，例如二次插值（quadratic interpolation formula，说实话我觉得中心差分的叫法不是很好，会让人联想到有限差分法FDM。仿照二次插值，中心差分完全可以叫做中心插值嘛），使用节点1，2，3的值来计算2、3交界面的梯度。数学上是这样实现的：
根据二次插值，设节点1、2、3之间的$\phi$分布为
$$\begin{equation} \phi = ax^2 + bx + c \end{equation}$$
那么考虑全部三个节点，可以写成：

$$\begin{equation} \left\{ \begin{matrix} x_1^2 & x_1 & 1 \\ x_2^2 & x_2 & 1 \\ x_3^2 & x_3 & 1 \end{matrix} \right\} \times \left\{ \begin{matrix} a\\b\\c \end{matrix} \right\} = \left\{ \begin{matrix} \phi_1 \\ \phi_2 \\ \phi_3 \end{matrix} \right\} \end{equation}$$
由上式可以写出$\phi$的分布，根据分布，控制面上的梯度是：
$$\begin{equation} \phi' = 2ax + b \end{equation}$$
显然，从西向东穿过控制面的通量，通过a、b两个量被节点1、2、3的值影响；从东向西的通量则被节点2、3、4的值影响。两者很难相同，这可能会带来守恒性的问题。

有界性

有界性的实现与代数方程组的对角占优性质有关。所谓对角占优（diagnolly dominant），指的是主对角元绝对值大于同一行其他元素绝对值之和的矩阵。即：

$$\begin{equation} \frac{\sum|a_{nb}|}{|a_p'|} \end{equation}$$
其中nb表示neighbour，$a_p'$表示对角元的净系数，也就是减去右侧源项向量之后的值(这个概念应该是针对齐次方程)。如果系数阵是对角占优的，那么P的值就应当被其边界值约束。
（对这一推论只是暂时给出一定性理解：假定W和E节点中有一个是0，比如W，那么P的值（绝对值）应小于E值的绝对值，这样就有界了。）

有界性的另一保障在于系数的符号。当系数的符号相同时，物理上就保证了一点值增加将导致其邻居值的增加。若符号相异，那么震荡的可能性就已经包含在矩阵中了。
之前只是照抄了书上的原话，现在才明白，这段话的意思是这样的：
所谓符号相同，指的是系数矩阵中$a_W$和$a_E$的符号相同，二者和$a_P$的符号相反。这样求解方程的时候，方程两边的符号才会相同，所以才会同时增减。

传输性

传输性，指的是离散格式在面对不同Pe数流场时的表现。Pe数表征对流和扩散的相对强弱。如果我们定义流动的通量为$F=\rho\boldsymbol{u}$以及扩散率（conductance）$D={\Gamma}/{\delta x}$，那么Pe数可以写为：

$$\begin{equation} Pe = \frac{F}{D}=\frac{\rho\boldsymbol{u}}{\Gamma/\delta x} \end{equation}$$

显然，当$Pe \to 0$时对流的作用可以忽略，扩散源的影响范围的是均匀的同心圆，反之扩散的作用只能影响到下游方向。

迎风格式

迎风格式的实现

如图所示，在使用5个node的情况下，迎风格式以一定的误差捕捉到了$\phi$场的变化趋势，而没有出现中心差分情况下的摇摆现象。迎风格式的优缺点将在下面被讨论。

迎风格式的评估

• 守恒性，有界性和传属性均可满足；
• 精度：迎风格式基于向后差分格式，因此只有一阶精度。根据安德森的教材我们直到，一阶精度对应数值扩散（false diffusion）。本书提到假扩散的现象，但是没有机理的详细分析，只给出了两篇年代久远的文献：
  
  • Leschziner, M. A. (1980). Practical Evaluation of Three Finite Difference Schemes for the Computation of Steady-state Recirculating Flows, Comput. Methods Appl.
    Mech. Eng., Vol. 23, pp. 293–312
  • Huang, P. G., Launder, B. E. and Leschziner, M. A. (1985). Discretisation of Non-linear Convection Processes: A Broad-range Comparison of Four Schemes,
    Comput. Methods. Appl. Mech. Eng., Vol. 48, pp. 1–24
    后续在处理数值扩散的问题时也许可以参考（例如VOF的数值扩散）。
    总而言之，迎风格式的一阶精度是不够实用的，我们显然需要更高精度的离散格式。

混合差分格式(hybrid differencing scheme)

混合格式的实现

1972年由Spalding提出，是一种结合了中心差分和迎风差分的格式。
核心思路在于根据Pe数修改离散格式：

$$\begin{equation} q_w = F_w[\frac{1}{2}(1+\frac{2}{Pe_w})\phi_W+\frac{1}{2}(1-\frac{2}{Pe_w})\phi_P] for -2<Pe_w<2\\ q_w = F_w\phi_W\\ q_w = F_w\phi_P \end{equation}$$
也就是在$|Pe|<2$时，使用中心差分离散计算面上变量值。此式可以化为：
$$\begin{equation} q_w = F(\frac{1}{2}(\phi_W+\phi_P))+D(\phi_W-\phi_P) \end{equation}$$
当$|Pe|\geq2$时只考虑对流影响，使用迎风格式即可。

混合格式的评估

• fully conservative
• unconditionally bounded
• transportiveness requirements are satisfied
• highly stable compared with heigher-order schemes such as QUICK
• only a 1st order scheme

power-law scheme

该方法由Patankar在1980年提出，被Fluent的momentum spatial discretization采用

power-law 格式的实现

$$\begin{equation} q = F[\phi_W - \beta_w(\phi_P-\phi_W)] for 0<Pe<10\\ where \beta_w = (1-0.1Pe_w)^5/Pe_w\\ and\\ q = F\phi_W for Pe>10 \end{equation}$$
即在$0<Pe<10$使用多项式逼近精确解（感觉很牛逼啊，为啥是这个5次方？幂律关系？可以找来原始文献看看）
在$Pe>10$使用迎风格式

power-law 格式的评估

作为hybrid scheme的替代，求解更精确。

上述两种使用了迎风格式的改进型格式仍然只有一阶精度。为了获取更高精度，首先考虑的是QUICK格式。