2016-Manica-The hydrodynamics of bubble rise and impact with solid surfaces

文献阅读笔记

---

离散相受力

added mass

added mass "arises because acceleration of the particle requires acceleration of the fluid. The volume of the 'added mass' of fluid is 0.5V, the same as obtained from potential flow theory."[1]
\begin{}

buoyancy

drag force

对具有immobile界面的气泡，例如被表面活性剂污染的气泡，速度无滑移，阻力符合stokes' law:

$$\begin{equation} F_D = 6\pi\mu \vec k \end{equation}$$
对mobile界面气泡，速度滑移，界面无切应力，阻力符合Hadamard–
Rybczynski的结果：
$$\begin{equation} F_D = 4\pi\mu \vec k \end{equation}$$

History force

This force is "originating from the unsteady diffusion of vorticity around the bubble"[2]

bubble velocity

terminal velocity

气泡平衡时，没有加速度，因此此时速度由drag force和buoyancy平衡得到。以气泡表面无滑移为例：

$$\begin{equation} V_T = \frac{2\rho gR^2}{9\mu} \end{equation}$$

rising velocity

气泡上升时的速度由上述力平衡方程控制，并最终收敛到terminal velocity。对力平衡方程无量纲化可求得其解析解。其中history force为变上限积分函数，对其无量纲化就是换元，因此积分上限跟着变化（以无滑移情况为例）：

$$\begin{equation} F_{history} = -6\pi\mu R\int_0^tG(t-\tau)\frac{dV}{d\tau}d\tau\\ = -6\pi\mu R\int_0^{t/t_s}G(t-\tau)\frac{dV}{d\tau}t_sd\tau^*\\ = -6\pi\mu R\int_0^{t^*}G(t-\tau)\frac{dV}{d\tau}t_sd\tau^*\\ \end{equation}$$
后续步骤跟其他项一样。即可得到其力平衡方程，为一积分-微分方程。两边求导可得到一二阶常微分方程。求解表明added mass 和 history force均显著。

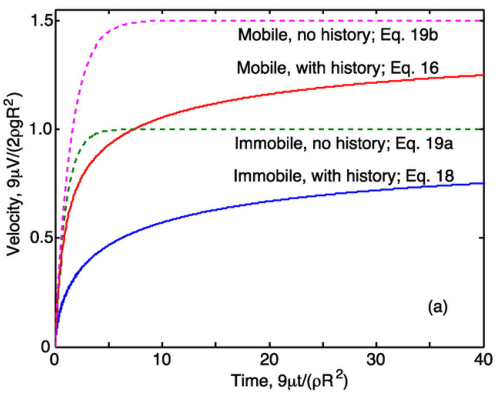
气泡接近平面时的阻力和速度

不涉及表面力的情况

对于自由液面和平壁面，阻力是相同的。
接近平面时，气泡受到的阻力为远场情况阻力乘一个系数：$F_D = 6\pi RV\lambda$，该系数在无滑移条件下的近似表达式为：

$$\begin{equation} \lambda = 1 + \frac RH + \frac38\frac{R}{R+H} \end{equation}$$
其中H为气泡距离自由液面的距离。

涉及表面力的情况

Van der Waals force

常在小于50nm的距离上起作用。此时（以immobile界面为例）$\lambda = R/H$。此时，半径分别为$R_1, R_2$的两个球（对于平板，半径为无穷）之间的范德瓦耳斯力可用下式描述，其中$E_{VDW}$是单位面积的Van der Waals能，$A$是hamaker常数，典型数值为$-10^{-19}J\sim -10^{-20}J$。负号表示静电排斥；计算等效半径的办法来源于

$$\begin{equation}Derjaguin approximation F_{VDW} = 2\pi R_{eff} E_{VDW}\\ E_{VDW} = -\frac{A}{12\pi H^2}\\ R_{eff} = \frac1{R_1} + \frac1{R_2} \end{equation}$$

electrical double layer force

同样在小于50nm的距离上起作用，在低浓度盐溶液中不可忽略（多么低？）。当$\kappa H_{eq}>1$（$H_{eq}$是平衡液膜厚度）时，在$\kappa H >2$（见下）的情况下可表示为：

$$\begin{equation} F_{EDL} = 2\pi R_{eff} E_{EDL}\\ E_{EDL} = -\frac1{\kappa}64n_0k_BT\tanh(\frac{e\psi_b}{4k_BT})\tanh(\frac{e\psi_s}{4k_BT})e^{-\kappa H} \end{equation}$$
其中：
$n_0$：一价电解质（monovalent (1:1) electrolyte）的数密度，单位为$mol/m^3$
$k_B$：玻尔兹曼常数
$T$：绝对温度
$1/\kappa$：德拜距离（Debye length）
$e$：元电荷
$\psi_B$：气泡的表面势surface potential
$\psi_S$：固体平板的表面势surface potential

表面力作用下的气泡运动

当气泡相当接近壁面时，表面力起作用而加速度几乎没有，此时added mass 和 history force可忽略。使用上述VDW、EDL和阻力的表达式，气泡受力为：

$$\begin{equation} 6\pi\mu R\lambda\frac{dH}{dt} = -\frac43\pi R^3\rho g - \frac{RA}{6H^2} + F_{EDL} \end{equation}$$
在较高浓度溶液中可忽略EDL力，则可求出位移与时间关系，对于immobile边界有:
$$\begin{equation} H(t) = \sqrt{\eta^2+(H_0^2-\eta^2)exp(\frac{-2t}{\tau})}\\ \eta = \frac{|A|}{8\pi\rho gR^2}\\ \tau = \frac{9\pi}{2\rho gR} \end{equation}$$