leidenfrost point 相关

文献阅读整理

---

几何关系

• capillary length[1]
  

  $$\begin{equation} a = \sqrt{\gamma/\rho g} \end{equation}$$

• the geometric Hertz relation[2]
  

  $$\begin{equation} \lambda \sim \sqrt{\delta R} \end{equation}$$
  其中$\delta$是"the lowering of the center of mass"，看了半天没看懂这是啥[3]。盲猜气膜厚度。此公式也见于其他文献[4]。

液滴下表面形状

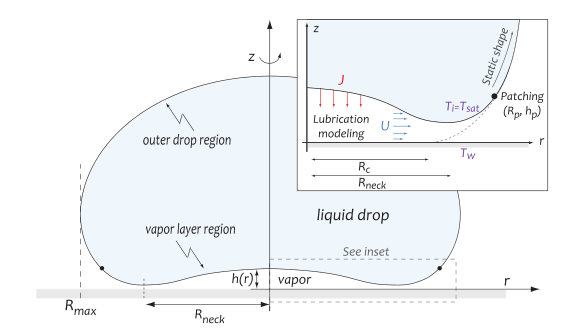
中心气膜最厚，沿半径方向减薄，然后重新升高。最薄处常被称为neck

Rayleigh-Taylor不稳定性

中心气膜最厚的现象可被Rayleigh-Taylor不稳定性描述，即密度较低的蒸汽倾向于处在密度较大的液体上方。液滴过大时，中心会浮出气泡[5]。

曲率与压力

对于轴对称的液滴，使用柱坐标系。设气膜厚度为$h$，则下表面的曲率为[6]：

$$\begin{equation} \kappa = \frac{h_{rr} + \frac1r(1+h_r^2)h_r }{(1+h_r^2)^{3/2}} \end{equation}$$
对于二维情况，曲率为：
$$\begin{equation} \kappa = \frac{h_{xx} }{(1+h_x^2)^{3/2}} \end{equation}$$
以向上为坐标系正方向，则弯曲的下表面提供的laplace压为：
$$\begin{equation} \Delta p = -\sigma \kappa \end{equation}$$
此公式计算的是界面弯曲和表面张力导致的压力跃升，不代表界面两侧压差就是这个数。只有稳态情况下二者才相等

气膜中的流动：Lubrication theory

LP稳态计算中不考虑润滑层中的惯性力，因此二维笛卡尔坐标系中动量方程和质量方程为[7]：

$$\begin{equation} p_x = \mu u_{yy}\\ p_y = 0\\ u_x + v_y = 0 \end{equation}$$
对动量方程积分，代入质量方程，可导出压力和厚度的关系[8]：
$$\begin{equation} \frac{\partial}{\partial x}(\frac{h^3}{12\mu}p_x) = \frac{\partial h}{\partial t} \end{equation}$$
上式在柱坐标系中应为[9]：
$$\begin{equation} \frac1r\frac{\partial}{\partial r}(r\frac{h^3}{12\mu}p_r) = \frac{\partial h}{\partial t} \end{equation}$$