boiling in porous media: model and simulations

文献阅读笔记

---

2005
JOHANN B´ENARD

Universit´e de Marne la Vall´ee

1.introduction

Applications:

• civil engineering applications
• petroleum engineering: water and vapor flooding
• nuclear reactor safety analysis: the storage or disposal of nuclear waste, which is difficult to manage accurate experiments for long-term storage.

Approach:

treating this problem consists in considering the various liquid phases as distinct fluids with individual thermodynamic and transport properties and with different phase specific fluxes.

简单来说就是分别处理两相

(Ramseh and Torrance, 1993) propose a model where interfaces separating single from two phase regions are tracked

追踪相界面

(Daurelle et al., 1998) propose a model where the liquid and the gaseous phases coexist in any point

混合模型

This model, which is an extension of (Wang and Beckerman, 1993; Ghafir, 2000; Najjari and Nasrallah, 2002) to cases where the energy equation cannot be written as an enthalpy balance, can be described by a set of equations, coupled with inequalities.

本文模型是前人模型[1]在能量方程不能写成焓平衡的情况下的推广。

2.description of the model

mass conservation and energy equations

• 多孔介质被看作一种独特的连续介质，由骨架和连续流体的叠加产生。
• 考虑三种物质：骨架，液体（水）和（水）蒸汽
• 局部热平衡（$T_s=T_l=T_v=T$）

conservation equations:

$$\begin{equation} \frac{\partial m_1}{\partial t} + \nabla\cdot (\rho_1v_1) = -\tau^w_{l \rightarrow v} \frac{\partial m_v}{\partial t} + \nabla\cdot (\rho_v v_v) = +\tau^w_{l \rightarrow v} \end{equation}$$

where

$$\begin{equation} m_l = \phi S \rho_l\\ m_v = \phi(1-S)\rho_v \end{equation}$$

$\phi$: porosity of porous medium
$S$: liquid saturation
$\tau^w_{l\rightarrow v}$: mass rate per volume unit transfered from l to v phase

energy equation:
能量方程的推导十分奇怪。具体过程可见coussy2004年的书籍[2]。在这里，作者直接使用了该书中的公式(6.11)，简化得到：

$$\begin{equation} \frac{\partial E}{\partial t} = -\nabla\cdot\sum(h_p\rho_p \vec v_p) -\nabla\cdot \vec q + \vec g \cdot \sum\rho_p\vec v_p + Q \end{equation}$$
其中，p指代不同的相（l：liquid或者v:vapor），h是焓，v是速度矢量，q是传热量，$\vec g$是重力加速度，Q是热源。

接下来作者写了一个后面没有用到的第二定律不等式，觉得没什么意义，暂不列。

接着，作者讨论了多孔介质中的耗散(dissipation)，一共分为三项，包括固有耗散(intrinsic dissipation)，流动耗散和传热耗散。文中给出了三者的表达式，但只有第一个用到了：

$$\begin{equation} \phi_{int} = T\frac{\partial \tilde{\eta}}{\partial t} -\frac{\partial E}{\partial t} - \sum g_p\nabla\cdot(\rho_p\vec v_p) \end{equation}$$
其中g为吉布斯势(gibbs potential)，$\tilde{\eta}$是总熵(total entropy):

$$\begin{equation} \tilde{\eta}=\phi S\rho_l\eta_l+ \phi(1-S)\rho_v\eta_v+ (1-\phi)\rho_s\eta_s \end{equation}$$

作者说：

Since the porous medium is assumed to be rigid, the intrinsic dissipation $\phi_{int}$ is equal to zero

所以，就可以根据总熵的表达式计算出能量的表达式。将之带入前述能量方程，可以得到方程(6)（原文编号）。方程（6）中的$\nabla\cdot(\rho_p\vec v_p)$使用质量守恒代换，并且假定相变过程中没有耗散（原文公式（7））,忽略体积力等，得到能量方程（原文方程（8））：

$$\begin{equation} T\frac{d\tilde{\eta}}{dt}+ \sum g_p\frac{dm_p}{dt} - \nabla\cdot(\sum h_p\rho_p\vec v_p) - \nabla\cdot\vec q+ Q \end{equation}$$
使用Fourier's law和Darcy's law，代换掉其中的q和v，即可获得所需的能量方程（原文11）。
质量方程只需将原有变量整理为待求量即可。
最终公式如下图所示：

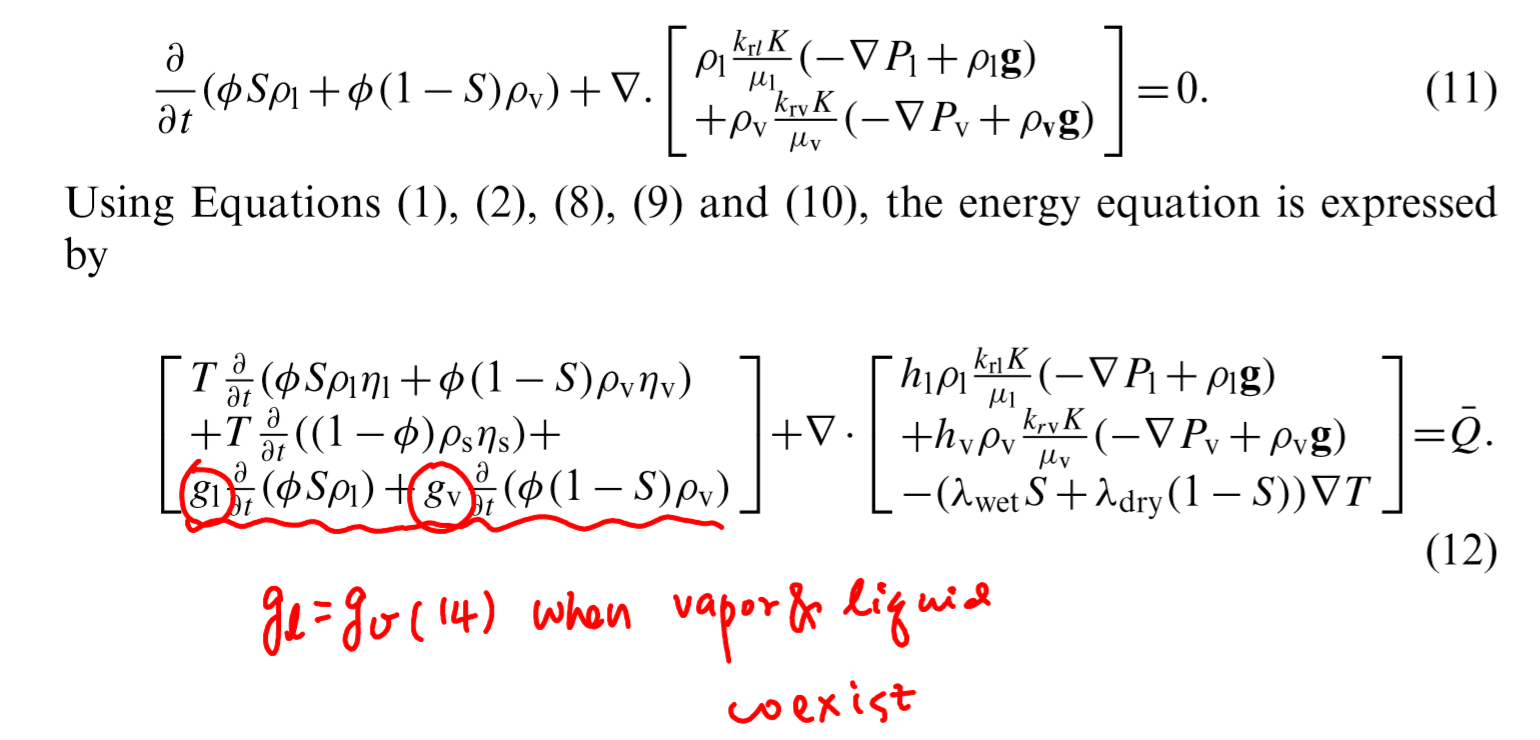
其中未知量为：$P_l,P_v,S,T$。因此为了封闭上述两方程，需要额外方程。其一是毛细压力方程：

$$\begin{equation} P_c(S) = P_v-P_l \end{equation}$$

另一方程则是关于gibbs potential的，作者引入如下关系：

然后作者表示上述四方程已封闭。未定的量例如$\tilde{\eta},h$根据后文的状态方程一节定出。

---

这个文章逻辑十分奇怪。看上去他的物性都是用方程计算得到的，而这些物性又是用实验值验证的。那么为什么不直接使用实验值呢？总熵的引入也是十分奇怪，没有见过把熵写进能量方程的方法。是不是要用焓作为自变量就一定会出现熵？然后熵和焓都以状态方程的形式计算得到？总之这种方法始终给人一种十分别扭的感觉。

而且这个文章透露着一种粗制滥造的感觉。图很简陋，公式漏写括号等号，还有一些写了没用到的公式。。总感觉像是凑字数的。但是文章难度并不低。emmmm矛盾的感觉。

暂时到这里吧，毕竟宏观模型并不是主要要看的内容。

---

初次阅读于：2019.07.16