The coalescen of bubbles in a pore body

菜鸡的草稿

---

The hydraulic resistance of the existing bubbles in the pore body to the subsequent bubbles is the reason for forcing flow diversion and flow pattern transformation. If the subsequent bubble expands fast enough, the liquid film between can be broken and the original upward flow can be maintained in the form of bubble coalescence. Otherwise, the gas has to flow laterally to achieve the nature of minimum flow resistance. As shown in the figure, the existing bubble has larger radius of curvature. The interface deformation of the existing bubble is not significant during the coalescence process.


The coalescence of bubbles in the pore body can be simplified as the dynamic process of a new bubble entering a pore body that has been partially occupied by the gas phase, as shown in the figure.

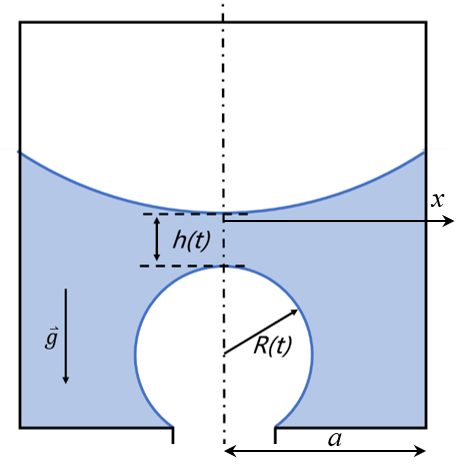
Hereby, the case of two-dimensional flow is discussed firstly. As a preliminary approximation, the existing gas phase can be considered stationary according to the experiments. The new bubble that shares the axis of symmetry with the existing bubble continuously expands under the effect of external pressure, and the liquid film between the gas phase is expelled to both sides, which is classified as a drainage process.

Governing equations:

When the bubbles are close to coalesce, the thickness of the liquid film is very thin compared to the curvature radius of the two gas-liquid interfaces, so the flow in it can be described using the lubrication model.

If inertial effects in the film can be neglected, the Navier–Stokes equations of the liquid between bubbles can be simplified to

$$\frac{\partial p}{\partial x} = \mu \frac{\partial^2u}{\partial y^2},\ \ \frac{\partial p}{\partial y} = 0,$$

where $\mu$ is the dynamic viscosity of the liquid phase, $h$ is the thickness of the liquid film.

Mass conservation law of the film can be writen as

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$$

Integrate the momentum equation and substitute the mass equation, one obtains the Reynolds equation for the problem:

$$\frac{\partial}{\partial x}(\frac{h^3}{12\mu}\frac{\partial p}{\partial x})=\frac{\partial h}{\partial t}$$

Under the premise that the viscous normal stress at the gas-liquid interface can be ignored[1], the pressure in the liquid film can be obtained from the gas phase pressure according to the Laplace equation:

$$p=p_{in}-\sigma\kappa$$
where $\kappa$ is the interface curvature, which reads:

$$\kappa=\frac{\partial^2h/\partial x^2}{(1+\partial h/\partial x)^{(3/2)}}$$

Assume that the deformation occur in a reigon of small interface slope, ie. $|\partial h/\partial r|\ll1$[2], film pressure reads:

$$p = p_{in} - \sigma\frac{\partial^2h}{\partial x^2}$$

Substitute Eq. above into Reynolds equation, one obtains an equation with 4th-order derivatives in x:

$$\begin{equation}\frac{\partial h}{\partial t}=\frac1{12\mu}\left[3h^2\frac{\partial h}{\partial x}(\frac{\partial p_{in}}{\partial x} - \sigma\frac{\partial^3 h}{\partial x^3})+h^3(\frac{\partial^2p_{in}}{\partial x^2}-\sigma\frac{\partial^4 h}{\partial x^4})\right]\end{equation}$$

The resistence exerted on the subsequent bubble reads:

$$F_r = 2\int_0^apdx$$

Initial and boundary conditions:

Since the interfaces only deform in a small area near the axis of symmetry[3],The film thickness distribution at the initial time can be approximated by a parabola. According to the pressure equation, the pressure in the liquid film can be calculated based on the two bubbles above and below, namely

$$p=p_1-\sigma\frac{\partial^2h_1}{\partial x^2}\\ p=p_2+\sigma\frac{\partial^2h_2}{\partial x^2}$$

The relationship between the pressure of the liquid film and the thickness of which can be obtained by the summation. Since the liquid film was not deformed at the time of the collision, thus the pressure is equal to the external pressure. Substitute $p = 0$ and integrate the formula twice to get its initial liquid film thickness distribution:

$$h = h_0+\frac{p_1+p_2}{4\sigma}x^2$$

Where $p_1 = \sigma / R_1$ is the pressure of the above bubble, and $p_2 = QR_gTt_0 / \pi R_2 ^ 2$ is the pressure of the below bubble, $h_0$ is the film thickness at the initial moment.

Far away from the film, Bubble's approach is controlled by its expansion, therefore $\partial h/\partial x$ is imposed and equals the formula about the expansion rate of the bubble:

$$\frac{\partial h}{\partial t}=(1-\frac{R}{\sqrt{R^2-x^2}})\frac{dR}{dt}$$

According to the Laplace's equation, the pressure in the bubble can be obtained based on the curvature radius of the main part of the bubble, that is, $p_ {in} = \sigma / R$, where the radius is a variable. Differentiate this formula to time:

$$\frac{dp}{dt} = -\frac{\sigma}{R^2}\frac{dR}{dt}$$

During the experiment, gas was injected into the experimental sample at a constant flow rate. Therefore, assuming that the flow rate $Q$ of the gas injection is constant, and the compressibility of the gas can be ignored, the expansion rate of the radius can be calculated using the gas flow rate:

$$Q = \frac{dm}{dt} = \rho 2\pi R\frac{dR}{dt}$$
Thus the pressure in the bubble can be obtained by integrating from the initial moment:
$$p_{in} = -\frac{\sigma Q}{2\pi \rho}\int_{t_0}^t\frac{1}{R^3}dt$$

Discretization of governing equation

Nondimensionalization

Using viscosity$\mu$, surface tension $\sigma$ and bubble interface expansion speed $V = dR/dt$ can define a dimensionless number, that is, the capillary number, which can be used to represent the relative magnitude of viscous force and surface tension:

$$Ca = \frac{\mu V}{\sigma}$$
the dimensionless form of the variables in the equation can be derived based on the capillary number:
$$\bar p = \frac{\sigma}{R_1}p, \bar{p_{in}} = \frac{R_1}{\sigma}p_{in}, \bar t = Ca^{1/2}\frac{\sigma}{R_1 \mu}t, \bar x = Ca^{-1/4}\frac{x}{R_1}.\bar h = Ca^{-1/2}\frac{h}{R_1}$$

$p_{in}$, the pressure in bubbles remains undetermined.

$$\frac{\partial \bar h}{\partial \bar t} = -\frac1{12}(3\bar h^2\frac{\partial \bar h}{\partial \bar x}\frac{\partial^3\bar h}{\partial \bar x^3}+\bar h^3\frac{\partial^4\bar h}{\partial \bar x^4})$$
$$\bar p = \bar p_{in} - \frac{\partial^2\bar h}{\partial \bar x^2}$$

其中，气泡内压力使用下式计算

$$p_{in}^{t+\Delta t} = p^t-\frac{\sigma Q}{2\pi \rho}\frac1{R^3}\Delta t$$
将上式无量纲化

Eq.(1) is linearized with respect to spatial coordinates $x$. A second-order accuracy finite difference scheme[5][6] is used to calculate the spatial derivatives in that equation:

$$\frac{\partial h}{\partial x} = \frac1{\Delta x}(-\frac12h_W+\frac12h_E)$$

$$\frac{\partial^2 h}{\partial x^2} = \frac{1}{\Delta x^2}(h_W-2h_P+h_E)$$

$$\frac{\partial^3 h}{\partial x^3} = \frac1{\Delta x^3}(-\frac12h_{WW}+h_W-h_E+\frac12h_{EE})$$

$$\frac{\partial^4 h}{\partial x^4}= \frac{1}{\Delta x^4}(h_{WW}-4h_{W}+6h_P-4h_E+h_{EE})$$

稳定性

spatial step	time step	velocity
5e-1	1e-5	-10
2e-1	1e-7	-10
1e-1	1e-8	-10

Discussion

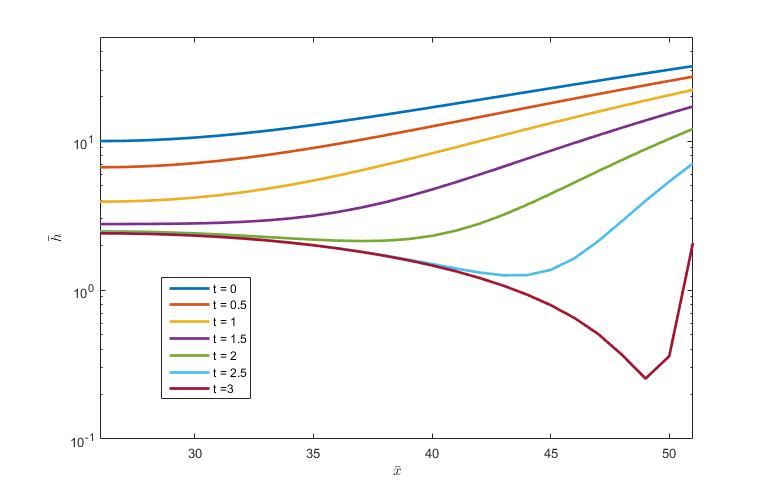
The evolution of the spatial distribution of liquid film thickness over time is shown in the figure.

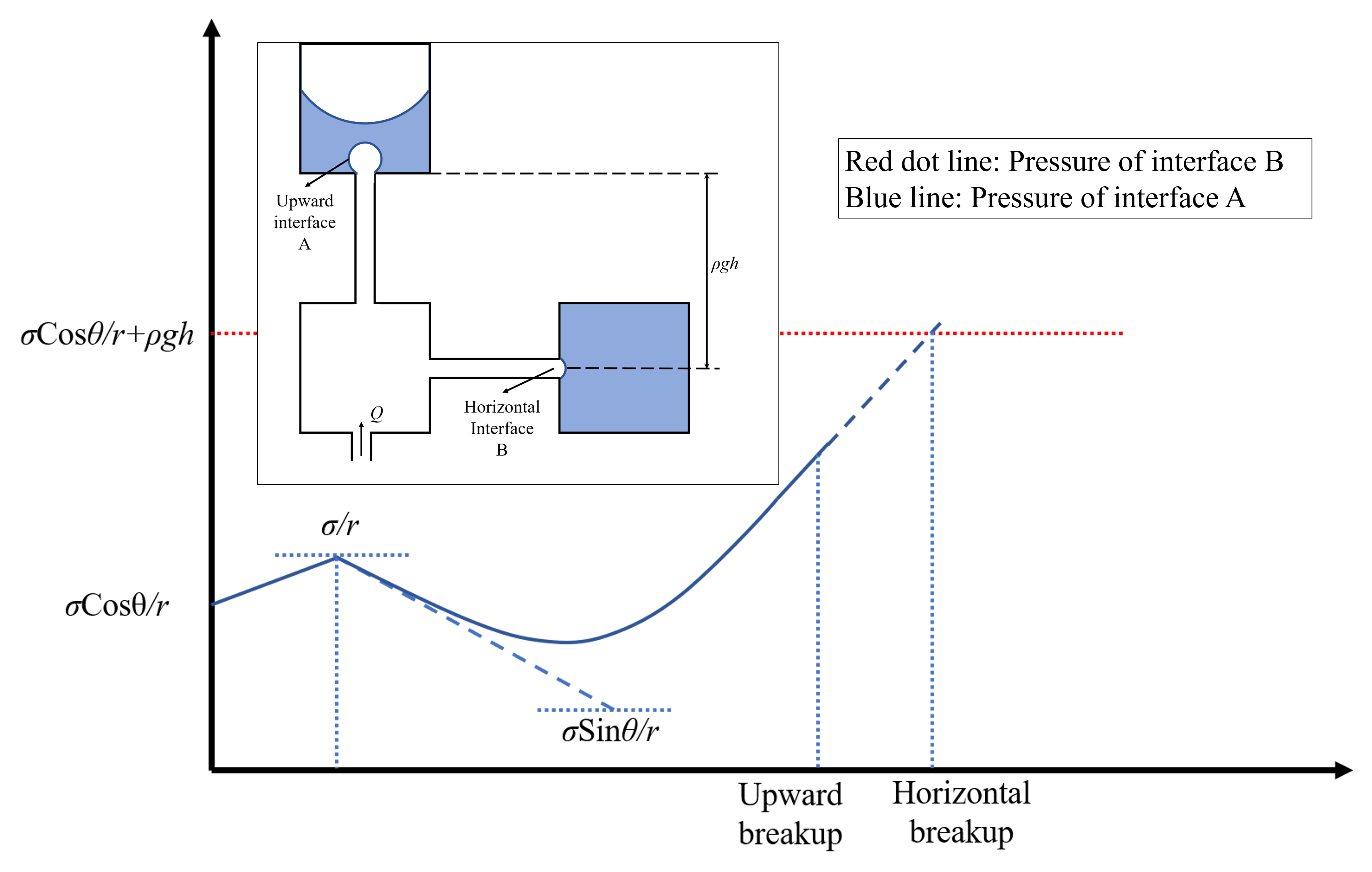
1. The calculation of entry pressure

$$\oint_{\Gamma}d\vec F = \int_{\Gamma_1}d\vec F + \int_{\Gamma_2}d\vec F$$
$$p_E = \frac{1}{\Gamma_2}\int_{\Gamma_1}\Delta p d\vec A$$
$$\bar{p_E} = \frac{\sum\bar{\Delta p}\bar{\Delta x}}{\sum\bar{\Delta x}} + \bar p_V$$
where, nondimensional pressure difference across the interface is
$$\bar{\Delta p} = \frac{\partial^2 \bar h}{\partial \bar x^2}$$
其中$\bar p_V$是液膜的运动压头，即$p_V = \rho u^2/4(R/\sigma)$
横向入侵的entry pressure包括毛细力和静水压力，即
$$\bar p_{EB}=\frac{\sigma cos\theta /r}{\sigma/R} + \frac{\rho g h}{\sigma/R}\sim 8$$

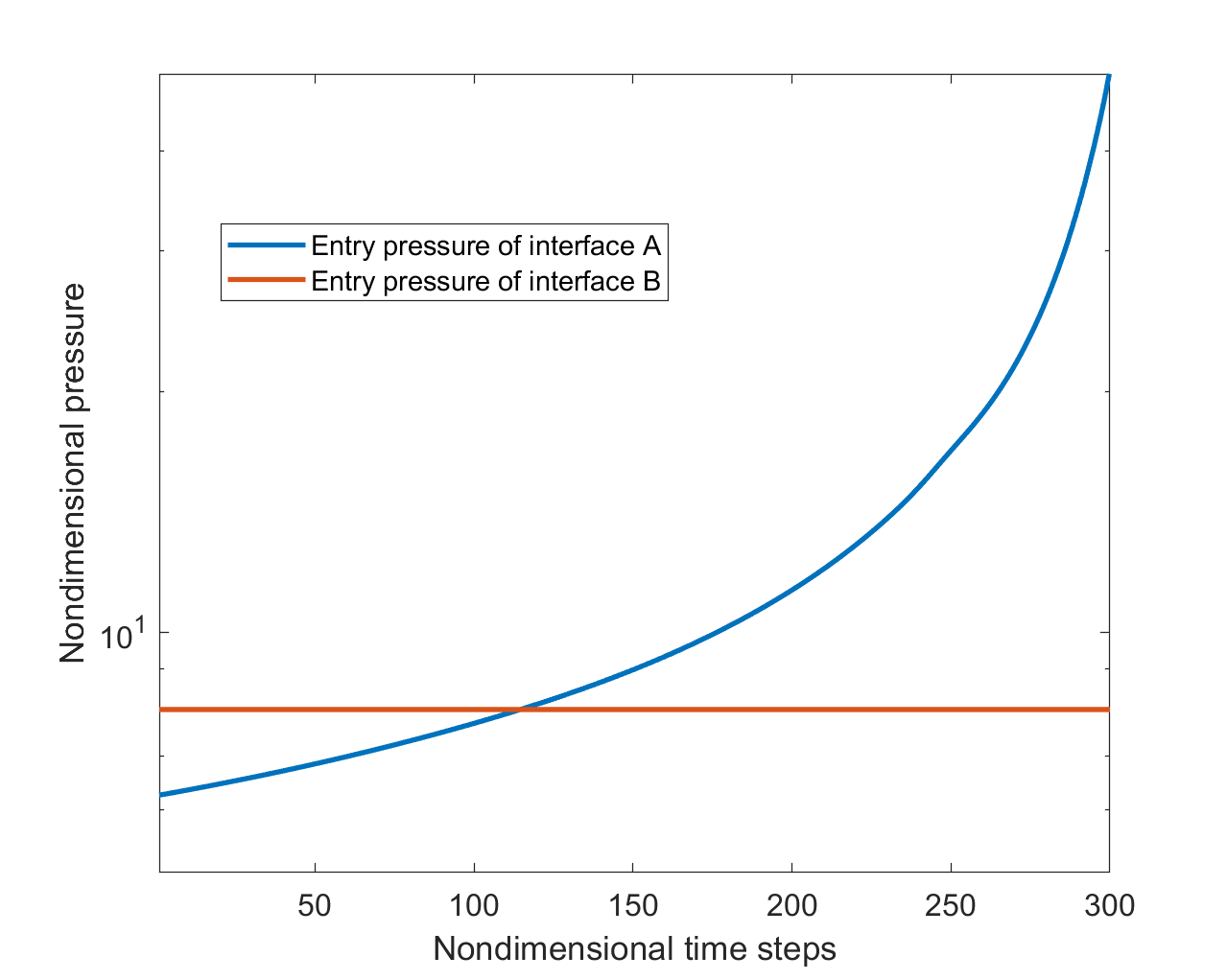
根据计算，此处entry pressure 大于横向入侵的entry pressure。由于惯性，二者同时入侵，假设平分流量。因此突破界面的选择借由入侵时间控制。

1. The calculation of critical time