2000-Klaseboer-Film Drainage between Colliding Drops at Constant Approach Velocity:Experiments and Modeling

文献阅读笔记

---

Introduction

• 影响气泡融合效率的两个时间尺度:

  • the contact time $t_c$which is mainly controlled by the exter-
    nal flow
  • the drainage time $t_d$ of the film thinning between drops until
    rupture by molecular forces
    融合是受分子级作用力控制的

• 界面边界条件（是否滑移）会导致多种regimes（参考文献3-6）

• 融合条件：恒速度（模拟惯性碰撞 参考文献7 有必要看看）和恒接触力（模拟浮力驱动）
• 现有实验多研究液滴与平板相互作用，有使用浮力驱动和使用液滴长大驱动（参考文献9-15*是如何长大的？与我的情况是否相同 很恐怖*）

Modeling the drainage process

Conditions

Governing equations

• NS方程：即半径方向和融合方向的动量方程（压力-速度方程）
  $$\frac{\partial p}{\partial r} = \mu(\frac{\partial ^2 u_r}{\partial z^2}),\ \ \frac{\partial p}{\partial z}= 0$$
  
  • 将前式积分两次，直接算不定积分，会有两个积分常数，使用条件$u_r = U\ for\ z = \pm h/2$即可求出速度曲线：
    $$u_r = U+\frac{1}{2\mu_c}\frac{\partial p}{\partial r}(z^2-\frac{h^2}{4})$$

第一项的速度是界面的径向速度引起的流动，也就是剪切流，也叫做plug flow或者Couette flow；第二项的二次分布，显然是个压力驱动流动，也就是Poiseuille flow。
+ 质量方程

如图所示选取微元体：

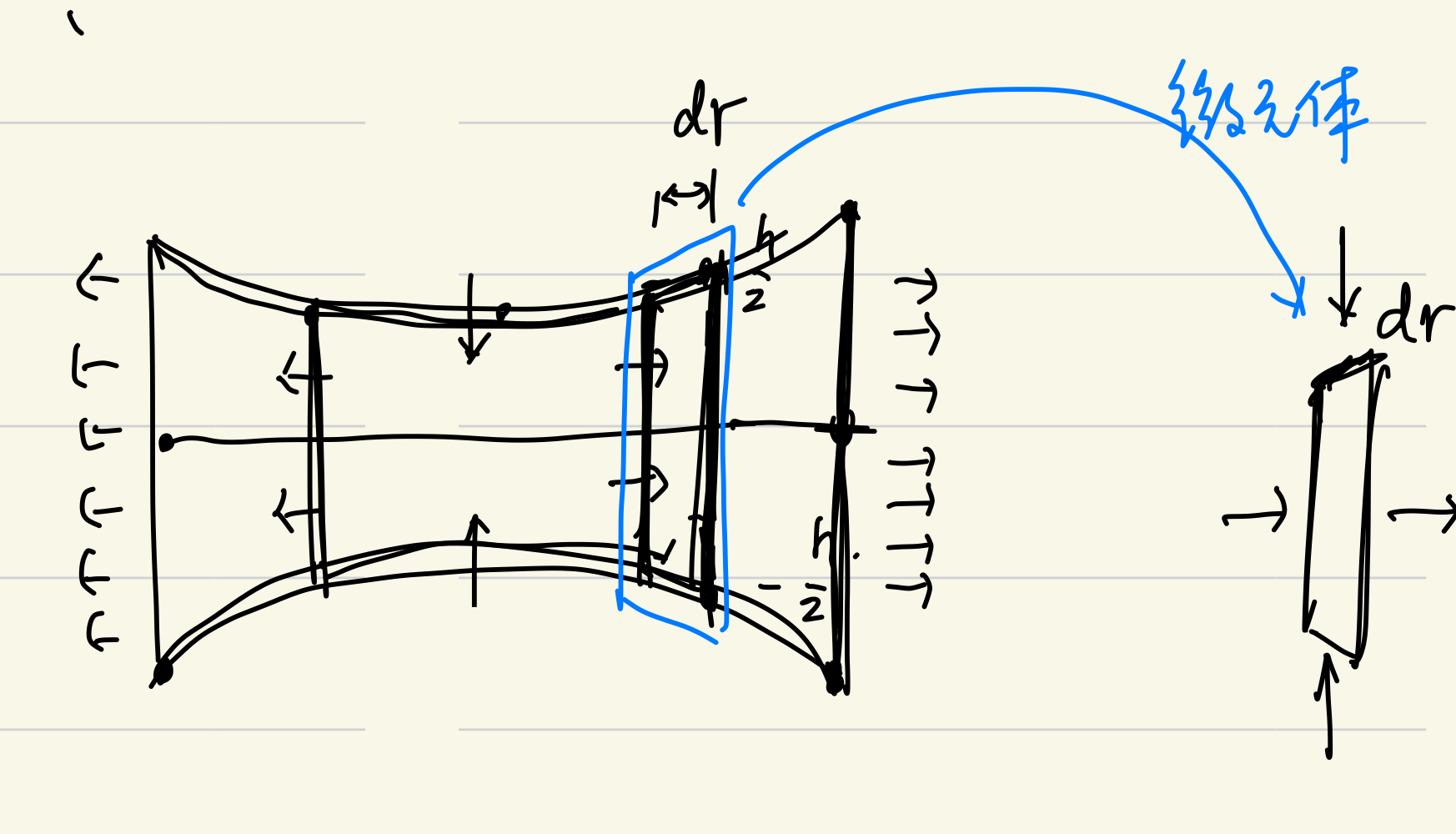
计算该微元体的净流出量，消去多余项：

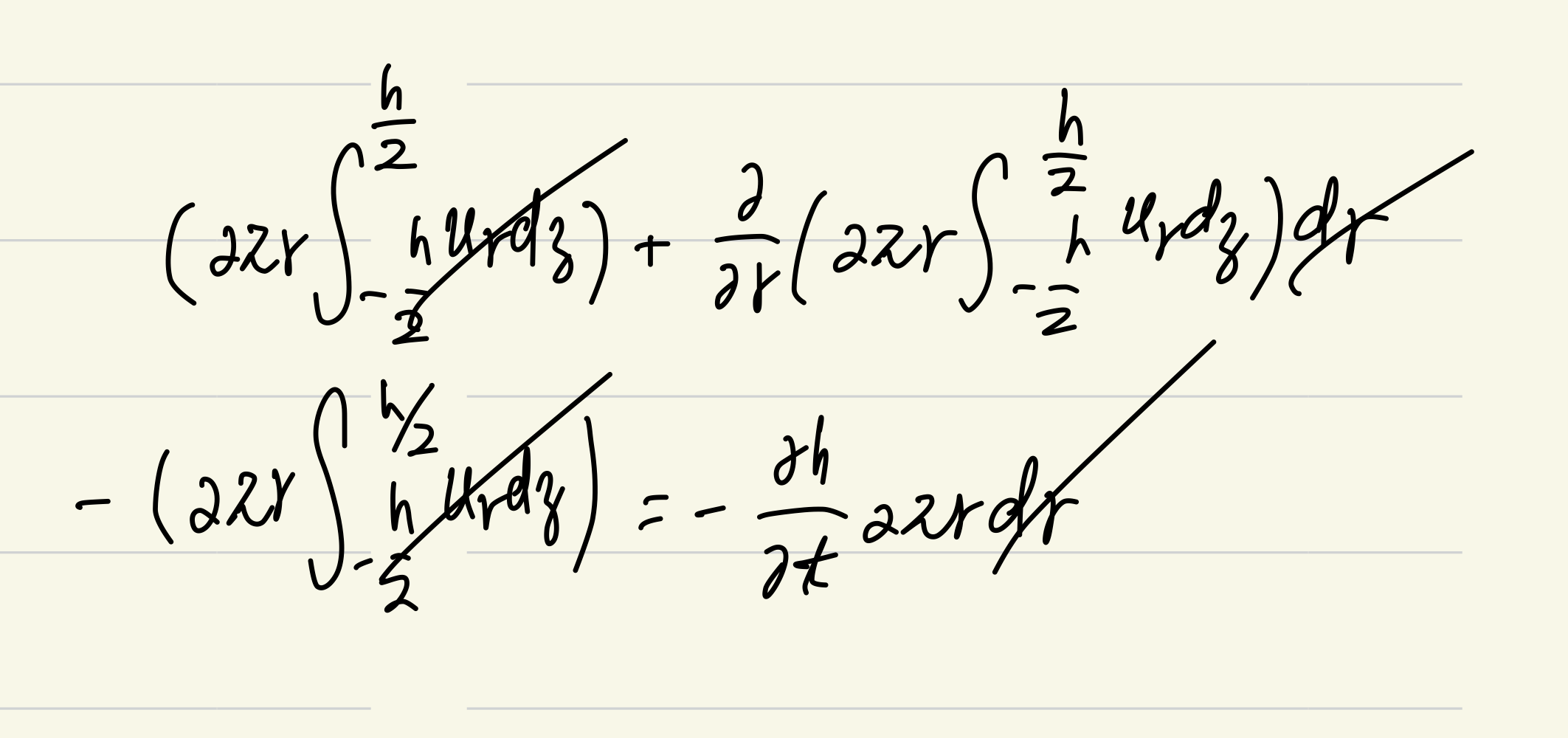
可以得到文中的质量方程

$$\frac{\partial }{\partial r}(2\pi r\int _{-h/2}^{h/2}u_rdz) = -2\pi r \frac{\partial h}{\partial t}$$

• Reynolds方程

所谓Reynolds方程，就是$h(t,r)$和$p(t,r)$的关系，所以只需要消去上式中的速度即可，而速度已经由NS方程积分得到，所以带入，有

$$\frac{\partial h}{\partial t} = -\frac1r\frac{\partial }{\partial r}(rUh)+\frac{1}{12\mu_c r}\frac{\partial}{\partial r}(rh^3\frac{\partial p}{\partial r})$$

其中第二项是我们所熟悉的三次方关系，前者则没有出现在我之前推过的表达式（见Leidenfrost相关公式8）这是因为第二项是Poiseuille flow 的结果，而第一项是速度方程中第一项Couette flow 的结果。Couette flow是界面水平速度的结果，以前的推导不考虑界面的水平速度则没有这一项（因为leidenfrost问题中液滴底部是静止的）。

如前所述，Reynolds方程是压力和液膜厚度的关系，这里有两个未知数，因此还需要一个方程进行封闭，这就是需要引入压力方程的原因。

一个值得注意的问题是，为什么质量+动量方程本身可以封闭，而由二者推出的Reynolds方程却不能封闭？原因在于原本的质量方程为$\nabla\cdot\hat v=0$，是一个单纯的速度方程，而此处的流场区域范围本身也是一个变量，也就是$h$，因为引入了一个多余的变量所以此处无法封闭。
+ 压力方程
以外流场的压力为0，那么根据Laplace公式计算液滴内的压力（第一项），再在此基础上，根据Laplace公式计算液膜的压力（第二项）

$$p = \frac{2\sigma}{R} - \frac{\sigma}{2r}\frac{\partial}{\partial r}(r\frac{\partial h}{\partial r})$$
以前好像没想明白以外流场压力为零这个计算基础

Initial and Boundary Conditions

• 初始界面形状
  这个问题显然是时间推进算法来解决的，必须先知道初始的界面形状。没有碰撞和融合的时候截面形状应该是圆形的，但是大家喜欢用抛物线近似来做。
  抛物线

关于初始截面形状，文献[1]中有比较详细的推导。
推导从Laplace方程开始。液膜和液滴之间的压力差写作：

$$p_d - p = \sigma(\frac1{R_a}+\frac1{R_b})$$
其中$1/R_a\ 1/R_b$分别是界面的主曲率半径

由于无穷远处液膜压力等于0，所以此处液滴压力等于$p_d = 2\sigma/R_i$，i指的是两个液滴中的一个。注意到右边是曲率的表达式，而圆柱坐标中的曲率写成(见Leidenfrost相关)：

$$\kappa = \frac{h_{rr} + (1+h_r^2)h_r /r}{(1+h_r^2)^{3/2}}$$

根据小变形假设，$h_r\ll 1$，所以$1+h_r^2\to 1$，所以上式变成：

$$\kappa = h_{rr} + \frac1r h_r = \frac1r\frac{\partial}{\partial r}(r\frac{\partial h}{\partial r})$$

所以有原文中的方程，根据液滴1写作：

$$p = \frac{2\sigma}{R_1} - \sigma(\frac{\partial^2h_1}{\partial r^2}+\frac1r\frac{\partial h_1}{\partial r})$$

根据液滴2写作：

$$p = \frac{2\sigma}{R_2} + \sigma(\frac{\partial^2h_2}{\partial r^2}+\frac1r\frac{\partial h_2}{\partial r})$$

注意到液膜厚度为$h=h_1-h_2$，所以将上二式求和，有

$$2p=2\sigma(\frac1R_1+\frac1R_2)-\sigma(\frac{\partial^2 h}{\partial r^2}+\frac1r\frac{\partial h}{\partial r})\\ p=\sigma(\frac1R_1+\frac1R_2)-\frac{\sigma}{2}(\frac{\partial^2 h}{\partial r^2}+\frac1r\frac{\partial h}{\partial r})$$

如果令$1/R_{eq} = (1/R_1 + 1/R_2)/2$，那么就有：

$$p=\frac{2\sigma}{R_{eq}}-\frac{\sigma}{2}(\frac{\partial^2 h}{\partial r^2}+\frac1r\frac{\partial h}{\partial r})$$
这个式子就是液膜压力和液膜厚度的关系，这个关系是适用于全过程的，但是里面有两个未知量，$p$和$h$，所以正常时候求解必须配合另一个方程进行封闭，这个配合的方程就是Reynolds方程。
显然，初始状态就是drop还没有变形，液膜中也没有压力的时候。此时$p=0$所以这个方程本身就可以确定液膜轮廓。因此带入压力为0，积分上式，可以得到：

$$h = h_0+\frac{r^2}{R_{eq}}$$

比较1989年文献[2]中的表达式（5）$h(r) = h_0 + r^2/2a$，可以看到上式右侧分母没有2的系数，原因在于1989年文献中的$a$为此处定义的$R_{eq}$的2倍，同样也是等效半径，而非真实drop的半径。