Non-local Neural Networks及自注意力机制思考

黄海安

---

论文地址：https://arxiv.org/abs/1711.07971 何凯明大佬挂名

1 创新点

  这篇文章非常重要，个人认为应该算是cv领域里面的自注意力机制的核心文章，语义分割里面引入的各种自注意力机制其实都可以认为是本文的特殊化例子。分析本文的意义不仅仅是熟悉本文，而是了解其泛化思想。

  不管是cv还是NLP任务，都需要捕获长范围依赖。在时序任务中，RNN操作是一种主要的捕获长范围依赖手段，而在CNN中是通过堆叠多个卷积模块来形成大感受野。目前的卷积和循环算子都是在空间和时间上的局部操作，长范围依赖捕获是通过重复堆叠，并且反向传播得到，存在3个不足：

  (1) 捕获长范围依赖的效率太低；

  (2) 由于网络很深，需要小心的设计模块和梯度；

  (3) 当需要在比较远位置之间来回传递消息时，这是局部操作是困难的.

  故作者基于图片滤波领域的非局部均值滤波操作思想，提出了一个泛化、简单、可直接嵌入到当前网络的非局部操作算子，可以捕获时间(一维时序信号)、空间(图片)和时空(视频序列)的长范围依赖。这样设计的好处是：

  (1) 相比较于不断堆叠卷积和RNN算子，非局部操作直接计算两个位置(可以是时间位置、空间位置和时空位置)之间的关系即可快速捕获长范围依赖，但是会忽略其欧式距离，这种计算方法其实就是求自相关矩阵，只不过是泛化的自相关矩阵

  (2) 非局部操作计算效率很高，要达到同等效果，只需要更少的堆叠层

  (3) 非局部操作可以保证输入尺度和输出尺度不变，这种设计可以很容易嵌入到目前的网络架构中。

2 核心思想

  由于我主要做2d图片的CV需求，故本文的大部分分析都是针对图片而言，而不是时间序列或者视频序列。

  本文的非局部操作算子是基于非局部均值操作而提出的，故很有必要解释下非局部均值操作。我们在CNN或者传统图片滤波算子中涉及的都是局部操作，例如Sobel算子，均值滤波算子等等，其计算示意图如下：

(图片来源：吴恩达深度学习课程)

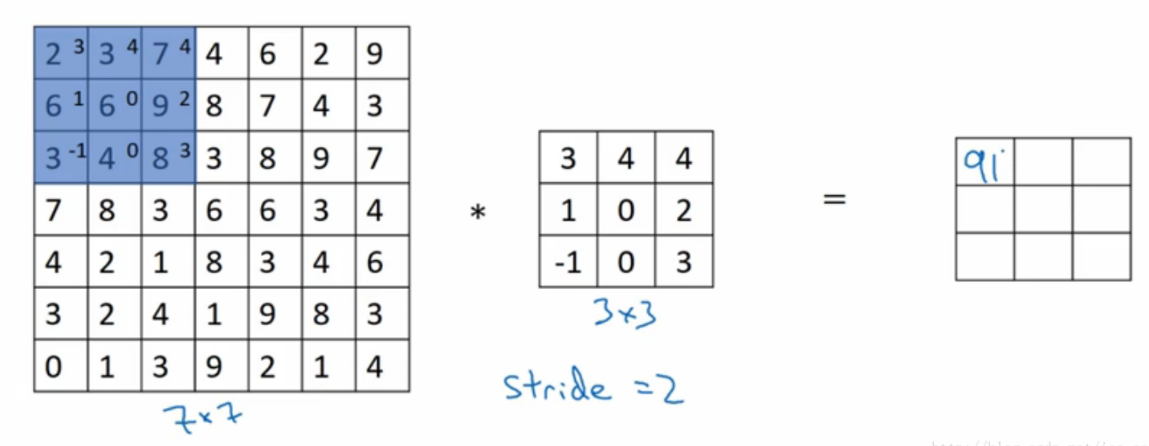
  可以看出每个位置的输出值都是kernel和输入的局部卷积计算得到的，而非局部均值滤波操作是： computes a weighted mean of all pixels in an image，非常简单。核心思想是在计算每个像素位置输出时候，不再只和邻域计算，而是和图像中所有位置计算相关性，然后将相关性作为一个权重表征其他位置和当前待计算位置的相似度。可以简单认为采用了一个和原图一样大的kernel进行卷积计算。下图表示了高斯滤波，双边滤波和非局部均值处理过程：

(图片来源：https://blog.csdn.net/wxz1120171495/article/details/81349391)

  可以看出对于待计算的中心红色点，前两种局部操作都是在邻域计算，而非局部均值是和整个图片进行计算的。但是实际上如果采用逐点计算方式，不仅计算速度非常慢，而且抗干扰能力不太好，故非局部均值操作是采用Block的思想，计算block和block之间的相关性。

  可以看出，待计算的像素位置是p，故先构造block，然后计算其他位置block和当前block的相关性，可以看出q1和q2区域和q非常相似，故计算时候给予一个大权重，而q3给予一个小的权重。这样的做法可以突出共性(关心的区域)，消除差异(通常是噪声)。

  上图可以看出非局部操作的优点，每一个例子中左图是待计算像素点的位置，右图是基于NL均值操作计算出来的权重分布图，看(c)可以非常明显看出，由于待计算点位置是在边缘处，通过非局部操作后突出了全部边缘。

  上面的所有分析都是基于非局部操作来讲的，但是实际上在深度学习时代，可以归为自注意力机制Self-attention。在机器翻译中，自我注意模块通过关注所有位置并在嵌入空间中取其加权平均值来计算序列（例如，句子）中的位置处的响应，在CV中那就是通过关注图片中(可以是特征图)所有位置并在嵌入空间中取其加权平均值来表示图片中某位置处的响应。嵌入空间可以认为是一个更抽象的图片空间表达，目的是汇聚更多的信息，提高计算效率。听起来非常高级的样子，到后面可以看出，是非常简单的。

3 网络结构

  下面开始给出非局部操作的具体公式。首先在深度学习中非局部操作可以表达为：

$$\mathbf { y } _ { i } = \frac { 1 } { \mathcal { C } ( \mathbf { x } ) } \sum _ { \forall j } f \left( \mathbf { x } _ { i } , \mathbf { x } _ { j } \right) g \left( \mathbf { x } _ { j } \right)$$

i是输出特征图的其中一个位置，通用来说这个位置可以是时间、空间和时空。j是所有可能位置的索引，x是输入信号，可以是图像、序列和视频，通常是特征图。y是和x尺度一样的输出图，f是配对计算函数，计算第i个位置和其他所有位置的相关性，g是一元输入函数，目的是进行信息变换，C(x)是归一化函数，保证变换前后整体信息不变。以上是一个非常泛化的公式，具体细节见下面。在局部卷积算子中，一般的$i − 1 ≤ j ≤ i + 1$。

  由于f和g都是通式，故结合神经网络特定，需要考虑其具体形式。

  首先g由于是一元输出，比较简单，我可以采用1x1卷积，代表线性嵌入，其形式为：

$$g\left( \mathbf { x } _ { j } \right) = W _ { g } \mathbf { x } _ { j }$$

  对于f，前面我们说过其实就是计算两个位置的相关性，那么第一个非常自然的函数是Gaussian。

(1) Gaussian

$$f\left( \mathbf { x } _ { i } , \mathbf { x } _ { j } \right) = e ^ { \mathbf { x } _ { i } ^ { T } \mathbf { x } _ { j } }$$

对两个位置进行点乘，然后通过指数映射，放大差异。

(2) Embedded Gaussian

$$f \left( \mathbf { x } _ { i } , \mathbf { x } _ { j } \right) = e ^ { \theta \left( \mathbf { x } _ { i } \right) ^ { T } \phi \left( \mathbf { x } _ { j } \right) }$$

前面的gaussian形式是直接在当前空间计算，而(2)更加通用，在嵌入空间中计算高斯距离。这里：

$$\theta \left( \mathbf { x } _ { i } \right) = W _ { \theta } \mathbf { x } _ { i }$$

$$\phi \left( \mathbf { x } _ { j } \right) = W _ { \phi } \mathbf { x } _ { j }$$

前面两个：$\mathcal { C } ( \mathbf { x } ) = \sum _ { \forall j } f \left( \mathbf { x } _ { i } , \mathbf { x } _ { j } \right)$

  仔细观察，如果把C(x)考虑进去，那么$\frac { 1 } { \mathcal { C } ( \mathbf { x } ) } f \left( \mathbf { x } _ { i } , \mathbf { x } _ { j } \right)$ 其实就是softmax形式，完整考虑是：

$$\mathbf { y } = \operatorname { softmax } \left( \mathbf { x } ^ { T } W _ { \theta } ^ { T } W _ { \phi } \mathbf { x } \right) g ( \mathbf { x } )$$

这个就是目前常用的位置注意力机制的表达式，所以说语义分割中大部分通道注意力机制都是本文的特殊化。

(3) Dot product

  考虑一种最简单的非局部操作形式：

$$f \left( \mathbf { x } _ { i } , \mathbf { x } _ { j } \right) = \theta \left( \mathbf { x } _ { i } \right) ^ { T } \phi \left( \mathbf { x } _ { j } \right)$$

其中C(x)=N，像素个数。可以看出(2) (3)的主要区别是是否含有激活函数softmax。

(4) Concatenation

  参考 Relation Networks可以提出：

$$f \left( \mathbf { x } _ { i } , \mathbf { x } _ { j } \right) = \operatorname { ReLU } \left( \mathbf { w } _ { f } ^ { T } \left[ \theta \left( \mathbf { x } _ { i } \right) , \phi \left( \mathbf { x } _ { j } \right) \right] \right)$$

前面是基本的非局部操作算子，利用这些算子，下面开始构造成模块。$\mathbf { z } _ { i } = W _ { z } \mathbf { y } _ { i } + \mathbf { x } _ { i }$

  可以看出，上面构造成了残差形式。上面的做法的好处是可以随意嵌入到任何一个预训练好的网络中，因为只要设置W_z初始化为0，那么就没有任何影响，然后在迁移学习中学习新的权重。这样就不会因为引入了新的模块而导致预训练权重无法使用。

  下面结合具体实例分析：

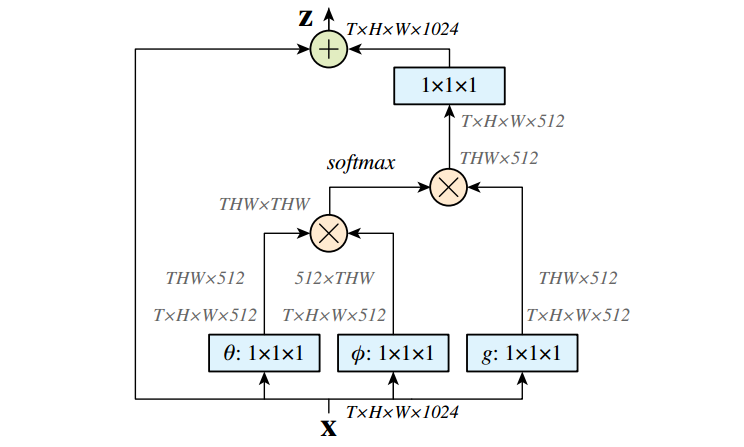
  由于我们考虑的是图片，故可以直接设置T=1，或者说不存在。首先网络输入是X=(batch,h,w,1024)，经过Embedded Gaussian中的两个嵌入权重变换$W_\theta,W_\phi$得到(batch,h,w,512),(batch,h,w,512),其实这里的目的是降低通道数，减少计算量；然后分别对这两个输出进行reshape操作，变成(batch,hxw,512)；然后对这两个输出进行矩阵乘(其中一个要转置)，计算相似性，得到(batch，hxw，hxw)；然后在第2个维度即最后一个维度上进行softmax操作，得到(batch,hxw,hxw)，注意这样做就是通道注意力，相当于找到了当前图片或特征图中每个像素与其他所有位置像素的归一化相关性；然后将g也采用一样的操作，先通道降维，然后reshape；然后和(batch,hxw,hxw)进行矩阵乘，得到(batch,hxw,512)，即将通道注意力机制应用到了所有通道的每张特征图对应位置上，本质就是输出的每个位置值都是其他所有位置的加权平均值，通过softmax操作可以进一步突出共性。最后经过一个1x1卷积恢复输出通道，保证输入输出尺度完全相同。

4 核心代码实现

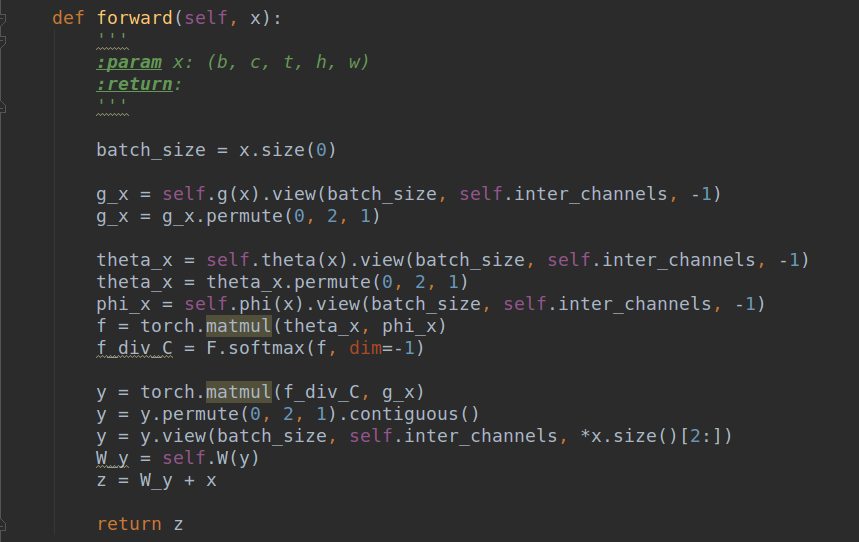
拷贝的代码来源：https://github.com/AlexHex7/Non-local_pytorch

可以看出，具体实现非常简单，就不细说了。

5 扩展

  通读全文，你会发现思路非常清晰，模块也非常简单。其背后的思想其实是自注意力机制的泛化表达，准确来说本文只提到了位置注意力机制(要计算位置和位置之间的相关性，办法非常多)。

  个人认为：如果这些自注意模块的计算开销优化的很小，那么应该会成为CNN的基础模块。既然位置和位置之间的相关性那么重要，那我是不是可以认为graph CNN才是未来？因为图卷积网络是基于像素点和像素点之间建模，两者之间的权重是学习到的，性能肯定比这种自监督方式更好，后面我会写文章分析。

  本文设计的模块依然存在以下的不足：

  (1) 只涉及到了位置注意力模块，而没有涉及常用的通道注意力机制

  (2) 可以看出如果特征图较大，那么两个(batch,hxw,512)矩阵乘是非常耗内存和计算量的，也就是说当输入特征图很大存在效率底下问题，虽然有其他办法解决例如缩放尺度，但是这样会损失信息，不是最佳处理办法。

  下一篇文章分析具有哪些扩展和新的改进策略。主要分析以下这些：