@huanghaian
2020-04-28T13:26:58.000000Z
字数 1811
阅读 1914
标定
3D视觉
1 张正友标定法
论文:A Flexible New Technique for Camera Calibration
1 小孔模型
假设2d图片上投影点坐标为,3d世界上坐标为,为了方便采用齐次方程计算,换成齐次坐标,,,小孔模型可以表示为:

s表示任意尺度,原因是2d平面上任意一点在3d平面上都是一条线,具有尺度不定性,故s无法估计。
R,t是旋转矩阵和平移向量,是世界坐标系到相机坐标系的转换矩阵。A是相机内参矩阵,
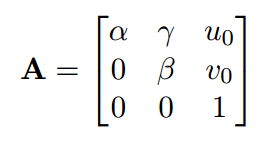
其中,γ描述两个像轴偏度的参数,一般都是接近0,或者直接设置为0也行。α和β是在图像u和v轴上的比例因子,就是焦距mm单位,(u0,v0)是主点坐标,主点存在的原因是像素坐标系(u,v)坐标和图片坐标系(x,y)存在坐标轴原点的平移。通常主点坐标是图片分辨率的一半(可以用来判断标定代码是否有问题),即像素坐标系的原点是成像平面的中心点,而图像坐标系原点是左上角。
2 估计单应矩阵
由于我们有精确的标定版,故设置世界坐标系原点为标定版上第一个角点上(可以检测出来),假设能够正确检测出所有标定版上面点,那么由于世界坐标系原点已知,标定板上面每个标定点的世界坐标都是已知了,也就是M坐标全部已知。现在采用角点检测算法也可以检测出图像坐标系的每个2d坐标m,那么利用方程(1)就可以求解出H了:
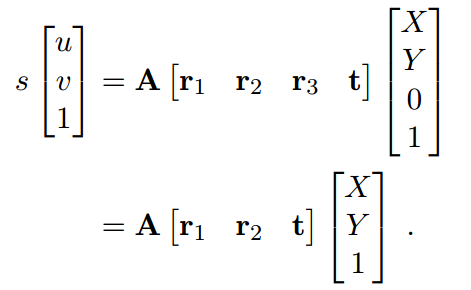

利用上述数据,就可以通过方程(2) 求解出H单应矩阵了。
具体求解过程为:
(1) 求闭式解
把s参数和H参数合并,相当于去掉了s尺度因子,
注意上述方程H是未知数,其余都是已知的。故设置
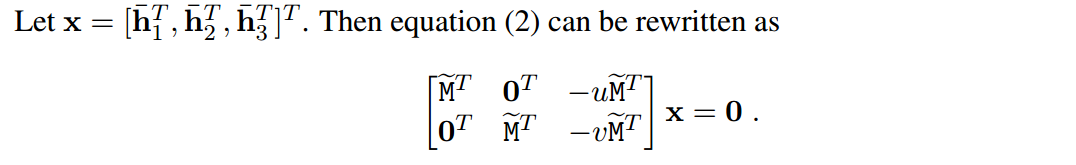
目的是求X,本质就是Lx = 0,假设一共有n个对应点,那么L就是2nx9的矩阵,Ax=0的矩阵解法非常简单,一步到位,其实就是矩阵的最小特征值对应的特征向量。考虑到可能存在病态矩阵,故实际上可以采用8点法求解。
(2) LM refine
上面的方程(2)实际上不一定成立,因为我们检测的角度实际上不可能那么准确,存在bias,导致方程不一定相等,也就是说上面得到的H值其实不准确,需要refine,常用的refine方法就是非线性最小二乘拟合(LM算法),假设检测的角点做法误差符合0均值的高斯分布
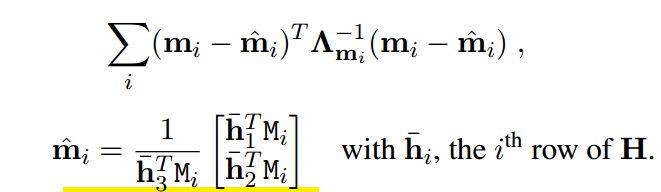
其中 ,非线性最小二乘是求解:
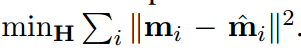
方程含义是2d投影误差最小。直接调用LM算法求解就好了,LM算法需要好的初始值,故采用上面得到的闭式解作为初始点即可。
3 求内参矩阵
现在已经得到了很好的H,H包含了A和旋转矩阵,现在需要利用H把每个变量求出来。
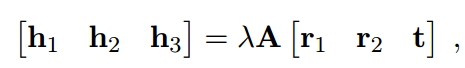
H矩阵可以写成上面的式子。
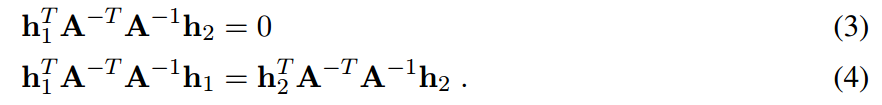
此时发现就只剩下A了,没有旋转相关参数了,是任意尺度因子。利用旋转矩阵正交的特性即向量r1和r2正交,可以得到上面2个式子。利用上面两个约束就可以求解上面所有需要的参数。注意H矩阵虽然是9个数,但是自由度是8,因为任意尺度,故可以设置任何一个变量为1,自由度就变成8了,求解办法也是一样,先求闭式解,然后refine。
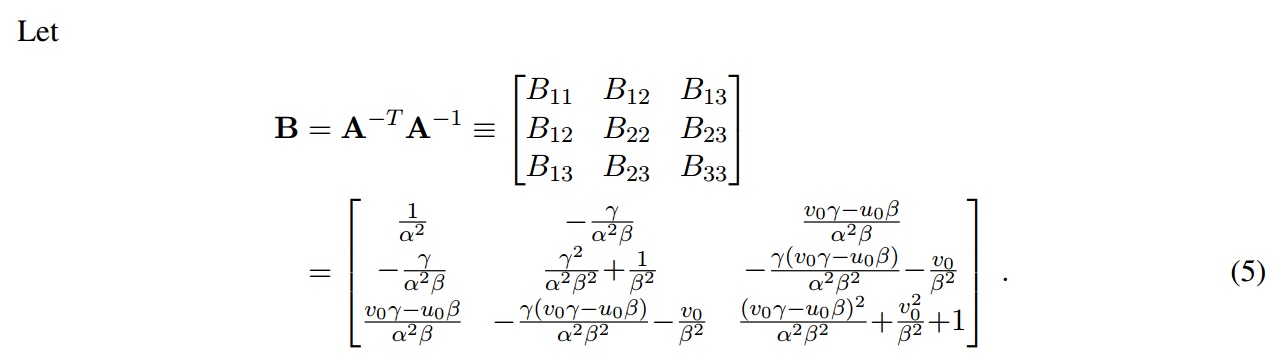
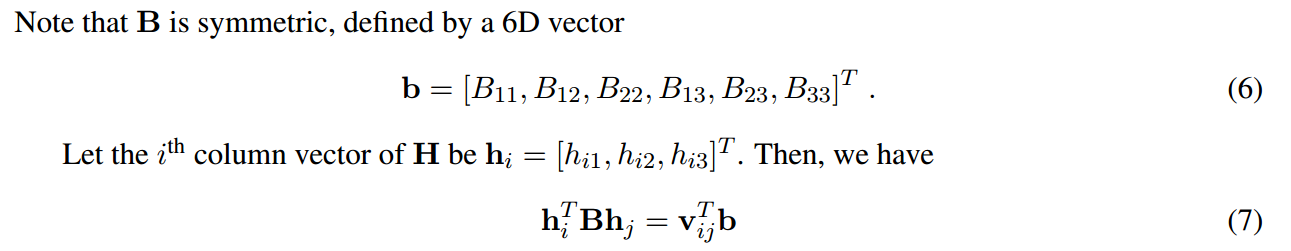
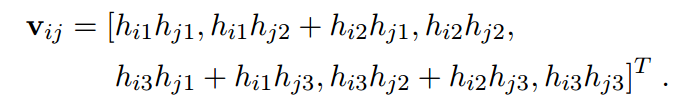
将(3)和(4)方程合并到一个矩阵内部,就得到:
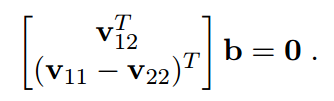
通式为:

V是2nx6的矩阵,可以看出B矩阵虽然是9个数,但是实际上自由度是5,为了求解方程,如果n大于等于3,那么肯定可以得到唯一解,且尺度因子也可以知道(相当于单目相机可以做双目的任务)。如果n=2,那么我们也可以设置偏斜可以设置为0,那么自由度下降一个,也可以求解出来了,如果n=1,那么就需要再次降低自由度,假设主点也已知,只求焦距即可。
注意上面的是理论值,也就是说要求解得到A,至少需要3张图片。但是3张图片估计肯定不准确的,一般需要20张左右。
求解b的过程,和前面一模一样,svd分解,最小奇异值对应的特征向量,进行LM refine。
4 求外参矩阵
A求出来了,那么其余参数也可以分解出来:
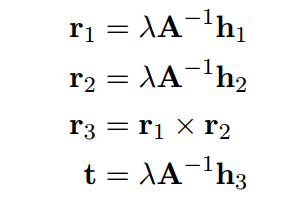
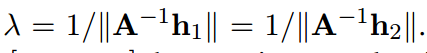
具体如何得到请看论文附录。
5 整体refine
上面那个参数都是单独refine得到了,为了提高精度,可以考虑将A和R,t的初始值带入LM算法中进行全局refine,
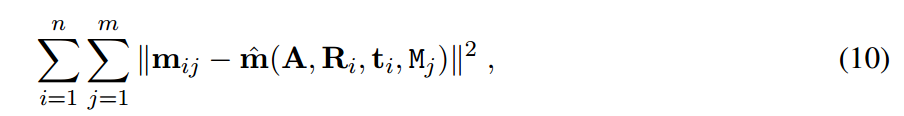
6 估计畸变参数
这个就比较简单了,对畸变进行建模,这里为了简单仅仅考虑径像畸变。

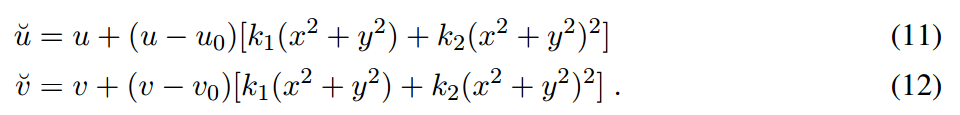
k1,k2就是要求解的参数,(x,y)是理想的没有畸变的坐标,是检测到的坐标,都是已知的,故求解上述方程就可以了,
最后全部参数统一refine:
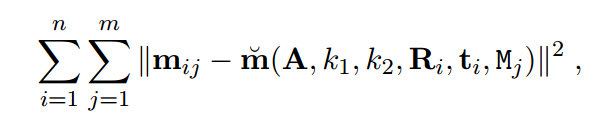
7 总结

后续需要结合opencv源码进行流程分析
