特征值分析

数学

---

特征值是线性代数中的一个领域。通过数据的一般格式来揭示数据的“真实”结构，即我们说的特征向量和特征值。

矩阵乘法的物理意义

矩阵乘法的物理意思是变换

A = np.matrix([[0,0],[1,0],[1,1],[0,1],[0,0]])
plt.plot(A[:,0],A[:,1])
plt.scatter(A[:,0],A[:,1])

伸缩

对应于主对角线上的值

B = np.matrix([[0.5,0],[0,3]])
C = A*B
plt.plot(A[:,0],A[:,1])
plt.scatter(A[:,0],A[:,1],color="red", label='A')
plt.plot(C[:,0],C[:,1])
plt.scatter(C[:,0],C[:,1],color="gray", label='A*B')
plt.legend()

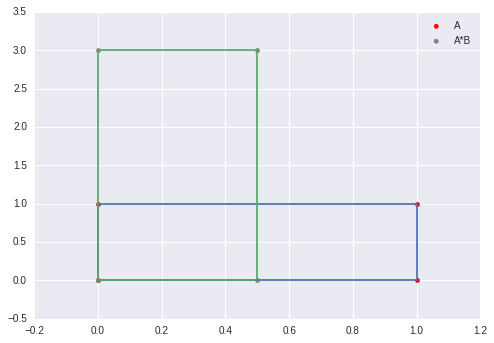
从图中可以看到x轴变为之前的0.5倍，而y轴变成了之前的3倍。

变换

而如果在矩阵B的某一列中除了主对角线外还有其他值，则相当于将所有点的该维度值发生一定变换。

B = np.matrix([[1,0],[1,1]])
C = A*B
plt.figure(figsize=(6,6))
plt.plot(A[:,0],A[:,1])
plt.scatter(A[:,0],A[:,1],color="red", label='A')
plt.plot(C[:,0],C[:,1])
plt.scatter(C[:,0],C[:,1],color="gray", label='A*B')
plt.xlim(-0.5,1.5)
plt.ylim(-0.5,1.5)
plt.legend()

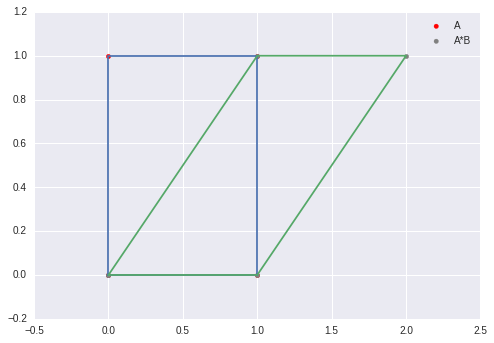
旋转

如果需要实现旋转，则需要准确计算矩阵

alpha = np.pi/6
B = np.matrix([[sp.cos(alpha),sp.sin(alpha)],[-sp.sin(alpha),sp.cos(alpha)]])
C = A*B
plt.figure(figsize=(6,6))
plt.plot(A[:,0],A[:,1])
plt.scatter(A[:,0],A[:,1],color="red", label='A')
plt.plot(C[:,0],C[:,1])
plt.scatter(C[:,0],C[:,1],color="gray", label='A*B')
plt.xlim(-0.5,1.5)
plt.ylim(-0.5,1.5)
plt.legend()

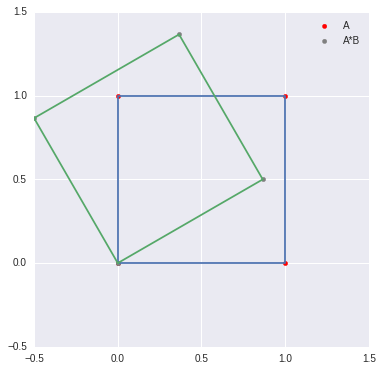
特征向量定义

N 维非零向量v是 N×N 的矩阵A的特征向量，当且仅当下式成立

$$Av=\lambda v$$ 其中λ为一标量，称为v对应的特征值。也称v为特征值λ对应的特征向量。也即特征向量被施以线性变换 A 只会使向量伸长或缩短而其方向不被改变。

向量变换

对于矩阵乘以向量，可以看着向量v为原坐标，而矩阵A为变化矩阵，则针对上面的三种变换为

v = np.matrix([[1],[1]])
A = np.matrix([[0.5,0],[0,3]])
B = np.matrix([[1,0],[1,1]])
C = np.matrix([[sp.cos(alpha),-sp.sin(alpha)],[sp.sin(alpha),sp.cos(alpha)]])
plt.figure(figsize=(6,6))
plt.scatter(v.T[:,0],v.T[:,1],color="red", label='v')
plt.scatter((A*v).T[:,0],(A*v).T[:,1],color="green", label='Av')
plt.scatter((B*v).T[:,0],(B*v).T[:,1],color="gray", label='Bv')
plt.scatter((C*v).T[:,0],(C*v).T[:,1],color="blue", label='Cv')
plt.xlim(0,3.5)
plt.ylim(0,3.5)
plt.legend()