SVM算法总结

机器学习 算法

---

拉格朗日乘子法和KKT条件

凸函数

所谓凸函数就是指函数的开口只有一个，要么向上，要么向下。其满足如下公式

$$\lambda f(x_1)+(1-lambda)*f(x_2)<f(x_1*\lambda + x_2*(1-\lambda))$$ 或
$$\lambda f(x_1)+(1-lambda)*f(x_2)>f(x_1*\lambda + x_2*(1-\lambda))$$
以下是对于函数$y=(x-1)^2$以及$y=-(x-1)^2$的图示，两者都是凸函数

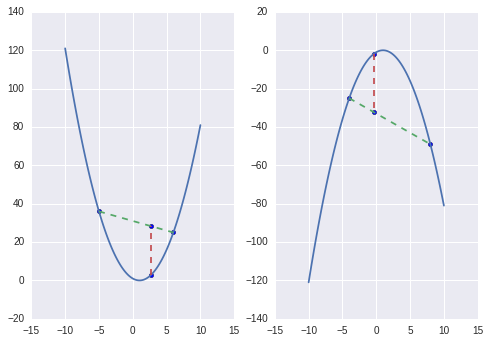
而对于函数$y=(x-1)^3$以及$y=-(x-1)^3$的图示，则不符合要求，不是凸函数

凸优化

由于函数是凸的，因此可以其要么只有一个最小值，要么就只有一个最大值（取决于凸的方向），因此求解该函数最小值和最大值的时候直接求导，就是全局最优解了。例如对于如下问题

$$f(x_1,x_2,x_3) = (x_1-1)^2 + 3*(x_2-2)^2 + 5*x_3^2 + 10，求\min f(x_1,x_2,x_3)$$ 则可直接通过求导可得 $${\partial f\over \partial x1}=2(x_1-1) = 0\rightarrow x_1= 1$$ $${\partial f\over \partial x_2}=6*(x_2-2)=0\rightarrow x_2=3$$ $${\partial f\over \partial x_3}=10*x_3=0\rightarrow x_2=3$$

带约束的凸优化

如果在刚才的问题添加上约束条件$x_1+x_2=5,x_2-3x_3=7$，其解又会咋样呢？正常情况下，在本题中可以通过将x2和x3用x1表示代入方程进行计算。

而应用拉格朗日乘子法，就是求解如下问题

$$\min f(x_1,x_2,x_3) = (x_1-1)^2 + 3(x_2-2)^2 + 5x_3^2 + 10+\alpha_1(x_1+x_2-5)+\alpha_2(x_2-3x_3-7)$$ 对其偏导可得 $${\partial f\over \partial x_1}=2(x_1-1)+\alpha_1=0\rightarrow x_1={2 - \alpha_1\over 2}$$ $${\partial f\over \partial x_2}=6(x_2-2)+\alpha_1+\alpha_2=0\rightarrow x_2 = {12-\alpha_1-\alpha_2\over 6}$$ $${\partial f\over \partial x_3}=14x_3-3\alpha_2=0\rightarrow x_3={3\alpha_2\over 14}$$ 将其带回约束条件，即可求得$\alpha_1,\alpha_2$进而求出最小值

针对f函数可以设想其等高线，而约束条件是一个平面，则其最优点即是平面与等高线相切的地方，如果是相交则其还有更小的等高线，由相切，则可知等高线和约束条件函数在该点具有相同的法向量。也即是说f的梯度与约束条件的梯度相同

$$\nabla f(x) = a\nabla g(x)\rightarrow \nabla (f(x)-ag(x)) = 0$$

KKT条件

如果约束条件是不等式怎么解决呢？假设有如下约束条件
$g_i(x)\le 0$
$h_i(x)=0$
那么由拉格朗日乘子法可转求该函数的最优解

$$L(x,\alpha,\beta)=f(x)+\sum\alpha_i g_i(x)+\sum\beta_ih_i(x)$$ 其最优解必定满足如下几个条件
1. $对各个x求导为0$
2. $h(x)=0$
3. $\sum\alpha_ig_i(x)=0,\alpha_i\ge0$，因为g(x)<=0，如果要满足该等式则必须要$\alpha=0$或者g(x)=0

函数变换

因为g(x)是小于0，而h(x)是等于0 的，所以我们通过调整$\alpha,\beta$可以得出下式 $$f(x)=\max_{\alpha,\beta}L(x,\alpha,\beta),[st:h(x)=0,g(x)<=0,\alpha>=0]$$ 因此 $$\min f(x)=\min_{x} \max_{\alpha,\beta} L(x,\alpha,\beta),[st:h(x)=0,g(x)<=0,\alpha>=0]$$

对偶最优化

我们有 $$d*=\max_{\alpha,\beta}\min_x L(x,\alpha,\beta)\le\min_{x} \max_{\alpha,\beta} L(x,\alpha,\beta)=p*$$ 为了通过求解对偶问题来求解前问题，则必须要满足如下假设
f和g是连续函数；h必须是仿射函数；g是严格可行的，表示肯定存在x使得对于所有i，g_i(x)都小于0
满足上面条件则证明必定有同解$(x^*,\alpha^*,\beta^*)$，而解会还会满足Karush-kuhn-tucker(KKT)条件：
1. $L(x^*,\alpha^*,\beta^*)对各个x求导为0$
2. $L(x^*,\alpha^*,\beta^*)对各个\beta求导为0$
3. $\sum\alpha^*_ig_i(x^*)=0$
4. $g_i(x^*)\le 0$
5. $\alpha_i^*\ge 0$

理解

因为是同解的， $$\min f(x)=\max_{\alpha,\beta}\min_x L(x,\alpha,\beta),[st:h(x)=0,g(x)<=0,\alpha>=0]$$ 因为对偶式中对L求的是x的极小值，因此L对各个x求导为0，而由对偶式的最外层是求最大，如果有$\sum\alpha_ig_i(x)!=0$，则由约束条件其必定小于0，因此我们可以通过改变$\alpha$使其等于0以取得更大的值，因此有$\sum\alpha_ig_i(x) =0$

线性支持向量机

线性分割平面与最大间隔

假设数据的分隔面是线性的，我们采用如下分离超平面

$$wx+b=0$$ 相应的分离决策函数就为 $$f(x)=sign(wx+b)$$ 则可以计算样本点与超平面的函数间隔为 $$\hat r_i=y_i(w\cdot x_i+b)$$ 由于函数间隔与w的范数相关，w、b同时变更时，分割面未变化，而函数间隔却发生变化，因此引入几何间隔 $$r_i = {1\over ||w||}y_i(w\cdot x_i+b)$$

硬间隔支持向量机

计算最大间隔

对于二分类问题，我们需要找到一个分割点使其完整的将数据划分成两类。我们设置分割平面为

$$wx+b=0$$ 在支持向量机这里我们则要求分割间隔最大，分割间隔如下 $$\max_{w,b} r;[s.t.\ y_i(w\cdot x_i+b)\ge\hat r]$$ 进一步变换 $$\max_{w,b} {\hat r\over||w||};[s.t.\ y_i(w\cdot x_i+b)\ge\hat r]$$ 取$\hat r = 1$ $$\max_{w,b} {1\over||w||};[s.t.\ y_i(w\cdot x_i+b)\ge 1]$$ 由于最大化$1\over ||x||$与最小化${1\over 2}||w||^2$是等价的，因此有： $$\min_{w,b} {1\over 2}||w||^2;[s.t.\ y_i(w\cdot x_i+b)-1\ge 0]$$

拉格朗日函数

构建拉格朗日函数，引入$\alpha$

$$L(w,b,\alpha)={1\over 2}||w||^2-\sum_{i=1}^N\alpha_iy_i(w\cdot x_i+b)+\sum_{i=1}^N\alpha_i$$ $$s.t. \ \alpha_i\ge 0,yi(w\cdot x_i+b-1)\ge 0,i\in[1...N]$$

根据KKT条件的第一条，函数L对w/b求导为0

$$\nabla_wL=w-\sum_{i=1}^N\alpha_iy_ix_i=0$$ $$\nabla_bL=\sum_{i=1}^N\alpha_iy_i=0$$
将结果代入L可得 $$L(w,b,\alpha)=-{1\over 2}\sum_{i=1}^N\sum_{i=j}^N\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)+\sum_{i=1}^N\alpha_i$$ 由$\min f = \max_{\alpha}\min_{w,b}L$得 $$\max_{\alpha}\min_{w,b} -{1\over 2}\sum_{i=1}^N\sum_{i=j}^N\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)+\sum_{i=1}^N\alpha_i$$
变换
$$\min_{\alpha}{1\over 2}\sum_{i=1}^N\sum_{i=j}^N\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)-\sum_{i=1}^N\alpha_i$$ $$s.t.\ \sum_{i=1}^N\alpha_iy_i=0;\alpha_i\ge 0$$

数据点分布

• $0\le \alpha_i$
• $\sum_{i=1}^N\alpha_iy_i = 0$
• $1-y_i(w\cdot x_i+b)\le 0$
• $\alpha_i(1-y_i(w\cdot x_i+b))=0$

当$\alpha_i\gt 0$ 则有$y_i(w\cdot x_i+b)=1$，数据位于边界上，为支持向量
当$\alpha_i=0$ 则有$y_i(w\cdot x_i+b)\ge 1$，数据位于边界或者之外

求解决策函数

根据上式求得最佳$\alpha^*=(\alpha_1^*, \alpha_2^*...)^T$

$$w^* = \sum_{i=1}^N\alpha_i^*y_ix_i$$ 选择任一$\alpha_j^*>0$ $$b^*=y_j-\sum_{i=1}^N\alpha_i^*y_i(x_i\cdot x_j)$$

软间隔支持向量机

引入松弛变量

对于线性不可分的数据集，则说明对于已划分好的分割超平面来说，某些点满足不了函数大于等于1的约束条件，为了解决这个问题，对于每个样本点引入一个松弛变量$\xi_i\ge 0$，这样使得函数间隔加上松弛变量大于等于1。约束条件就变为：

$$y_i(w\cdot x_i+b)\ge 1-\xi_i$$
从该式中我们可以看到$\xi_i$的取值情况对点位置的影响

• $\xi_i=0$ 则允许数据点位于边界以及边界之外，具体取决于实际值
• $0<\xi<=1$ 则允许该数据点在边界内，分类正确
• $\xi_i>1$ 则允许该数据点分类错误

引入惩罚参数C

同时对于引入的每个松弛变量，支付一个代价$\xi_i$，则目标函数变为

$${1\over 2}||w||^2+C\sum_{i=1}^N\xi_i$$ 从等式中可以看到分错的点和边界内的点越多，则$\sum_{i=1}^N\xi_i$的值就越大，因此C就相当于控制对分错点的容忍程度，如果C的值越大，则分类更严格，C变少，则通过将更多的放在边界内或分错而达到更大的分割间隔。

对偶算法

新的目标函数的拉格朗日函数如下

$$L(w,b,\xi,\alpha,u)={1\over 2}||w||^2+C\sum\xi_i-\sum\alpha_i(y_i(w\cdot x_i+b)-1+\xi_i)-\sum u_i\xi_i$$
其对w/b/$\xi$求导得 $$\nabla_wL=w-\sum_{i=1}^N\alpha_iy_ix_i=0$$ $$\nabla_bL=-\sum_{i=1}^N\alpha_iy_i=0$$ $$\nabla_{\xi_i}L=C-\alpha_i-u_i=0$$

代入原式根据对偶问题可得

$$\min_{\alpha}{1\over 2}\sum_{i=1}^N\sum_{i=j}^N\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)-\sum_{i=1}^N\alpha_i$$ $$s.t.\ \ \ \ \sum_{i=1}^N\alpha_iy_i=0;\alpha_i\ge 0;u_i\ge 0;C-\alpha_i-u_i=0$$ 消除u可得 $$s.t.\ \ \ 0\le \alpha_i \le C$$

数据点分布

• $0\le \alpha_i \le C$
• $\sum_{i=1}^N\alpha_iy_i = 0$
• $1-\xi_i-y_i(w\cdot x_i+b)\le 0$
• $\alpha_i(1-\xi_i-y_i(w\cdot x_i+b))=0$

当$\alpha_i=0$ 则分类正确
当$0\lt \alpha_i\lt C$ 则有$u_i > 0，\xi_i = 0$，数据位于边界上，为支持向量
当$\alpha_i=C$ 则有$u_i=0$，则需要根据$\xi_i$的值进行判断

• $0\lt \xi_i\lt 1，则有0\lt y_i(w\cdot x_i+b) \lt1$，则数据分类正确，位于间隔边界与分离超平面之间
• $\xi_i = 1，则有\ y_i(w\cdot x_i+b) =0$，数据位于分离超平面上
• $\xi_i > 1，则有\ y_i(w\cdot x_i+b) <0$，数据位于超平面误分一侧

求解决策函数

根据上式求得最佳$\alpha^*=(\alpha_1^*, \alpha_2^*...)^T$

$$w^* = \sum_{i=1}^N\alpha_i^*y_ix_i$$ 选择任一$0\le \alpha_j^*\le C$ $$b^*=y_j-\sum_{i=1}^N\alpha_i^*y_i(x_i\cdot x_j)$$

非线性支持向量机

核函数

SMO算法

根据上面的分析，实际上是求如下极值 $$min W(\alpha)=\min_{\alpha}{1\over 2}\sum_{i=1}^N\sum_{i=j}^N\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)-\sum_{i=1}^N\alpha_i$$

约束条件

$0\le \alpha_i \le C$
$\sum_{i=1}^N\alpha_iy_i = 0$
$1-y_i(w\cdot x_i+b)\le 0$
$\alpha_i(1-y_i(w\cdot x_i+b))=0$

SMO方法是迭代方法，每次迭代调整分错的点直到收敛；在迭代过程中，会有3种点，第一种
- y(wx+b) > 1 已分对的点，其alpha为0，可以不调整
- y(wx+b) = 1 支持边界上的点

不满足条件的点：
yu <= 1 但是 alpha < C
yu >= 1 但是 alpha > 0
yu <= 1 但是 alpha = 0 或者 alpha = C

同时改变2个alpha

因为是求函数的最小值，核心思想是一次只在一个维度上使得函数最大化，其循环次数可能会较多，但是循环内部比较简单。由于约束$\sum_{i=1}^N\alpha_iy_i = 0$存在则我们不可能一次只改变一个而满足等式，因此我们每次改变两个坐标。假设选择如下两个则有：

$$\alpha_1y_i+\alpha_2y_2= - \sum_{i=3}^N\alpha_iy_i=v\rightarrow \alpha_1=(v-\alpha_2y_2)y_1$$ 则最小值函数变为 $$W((v-\alpha_2y_2)y_1，\alpha_2...)={1\over 2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)-\sum_{i=1}^N\alpha_i$$ $$=a\alpha_2^2+b\alpha_2+c$$ 可对其求导即可得$\alpha_2$的值，因为$\alpha_2$的取值有0到C的限制，因此选择合适的值，同时由于$\alpha_1$的取值限制，可能还需要再次调整$\alpha_2$的值（这里可以先通过$\alpha_1$的取值范围对$\alpha_2$的取值范围进行限制）

第一个alpha选择

第一个alpha就是选择样本点最不满足KKT条件的:

$$\alpha_i=0\iff y_ig(x_i)\ge 1$$ $$0\lt \alpha_i\lt C\iff y_ig(x_i)=1$$ $$\alpha_i=C\iff y_ig(x_i)\le 1$$ 其中 $$g(x_i)=\sum_{j=1}^N\alpha_jy_jK(x_i,x_j)+b$$
优先选择位于0～C之间的点判断，再选择整个训练集

第二个alpha选择

第二个alpha选择的标准是希望alpha2有足够大的变化。由于alpha2是依赖于两个alhpa对应的点误差的绝对值，因此可以选择该值最大的。

代码实现

Github：https://github.com/spiritwiki/codes/tree/master/svm
coding.net：https://coding.net/u/spiritwiki/p/codes/git/tree/master/svm

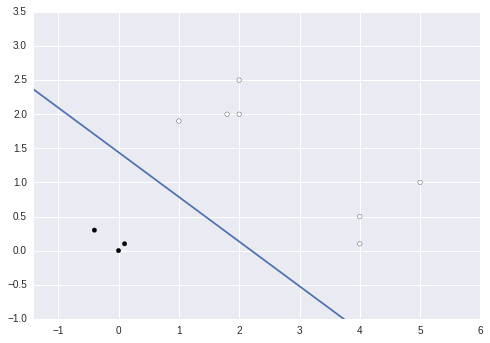
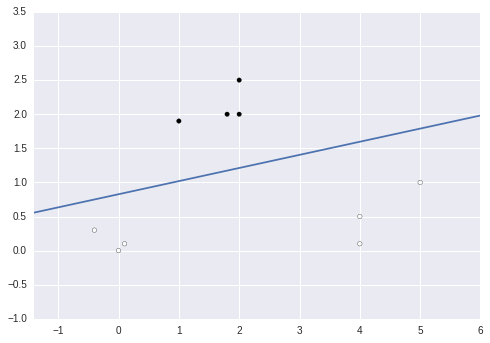
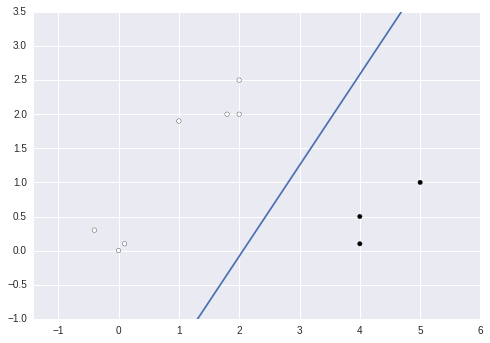
线性分类

针对简单测试集其分类图如下