概率基础

数学

---

1 计数

分类计数原理（加法原理）

完成一件事，有n类方法，第i类方式中有ni种不同方法，那么完成这件事总共的方法数为

$$\sum n_i$$

分步计数原理（乘法原理）

完成一件事，需分成n个步骤，做第i步有ni种方法，那么完成这件事的方法数为

$$\prod n_i$$

有序的重复抽样

如果样本空间总数为n，抽样m次，则总的抽样可能性为

$$n^m$$

有序的非重复抽样

有序的非重复抽样又叫做排列(permutation)。从数学上来说，从n个样品中挑选m个，放入m个位置，总可能性为

$$n!\over (n-m)!$$

无序的非重复抽样

无序的非重复抽样又叫做组合(combination)

$$C(n,m) = {n! \over m!(n-m)!}$$

无序的重复抽样

也即是考虑将m次抽样分别放入n个样本空间的组合，允许其大于等于0，也即是相当于找出n-1的间隔将抽样隔开

$$C(m+n-1,n-1) = {(m+n-1)!\over (n-1)!m!}$$

2 概率公理

实验

任何一个过程，如果它的结果是随机的(无法事前知道)，那么该过程就称为一个实验。实验所有可能的结果组成一个集合(set)，叫做样本空间(sample space)，用Ω表示

事件

在实验中，我们感兴趣的往往不是单个可能，样本空间的一个子集，被称为一个事件(event)

• 补集，事件A的补集包含所有不属于A的样本空间元素
• 两个集合可以有交集和并集运算
• 空集Φ是一个不包含任何元素的集合。如果两个集合的交集为空集，即M∩N=Φ，那么这两个集合不相交。在概率论中，不相交的两个事件互斥。

概率测度

概率测度是基于样本空间ΩΩ的一个函数P。这个函数P定义了从样本空间的子集(即事件)到实数的映射，且满足下面的条件:

1. P(Ω)=1P(Ω)=1
2. 如果A⊂ΩA⊂Ω, 那么P(A)≥0P(A)≥0
3. 如果A1A1和A2A2不相交，那么 $$P(A1∪A2)=P(A1)+P(A2)$$

3 条件概率

定义

如果A和B是两个事件，且P(B)≠0。那么B条件下，A的条件概率为 $$P(A|B)={P(A∩B)\over P(B)}$$

推论1

A和B为两个事件，且P(B)≠0。那么 $$P(A∩B)=P(A|B)P(B)$$

推论2

有事件B1,B2,...,Bn。如果⋃Bi=Ω，两个不同事件互斥(Bi∩Bj=Φ,Bi如果i≠j），且任意P(Bi)>0。那么，对于任意事件A $$P(A)=\sum_{i=1}^nP(A|B_i)P(B_i)$$

独立事件

两个事件可以是相互独立的 (independent)。直观的讲，如果事件A发生与否不会影响事件B的概率，那么A与B独立。

定义

两个事件A和B，P(A)≠0，P(B)≠0。如果P(A|B)=P(A)，或者P(B|A)=P(B)，那么事件A和B是独立事件

根据独立事件和条件概率的定义可以推知，如果P(A∩B)=P(A)P(B)，那么A和B独立。独立事件和互斥事件不同。独立事件是指A发生的概率不影响B。对于互斥事件来说，如果A发生，那么B必然不发生，A的发生影响到了B，所以不是独立事件。

贝叶斯法则(Bayes' Rule)

贝叶斯法则

如果A和B1,B2,...,Bn为事件，Bi互斥，⋃Bi=Ω， 且P(Bi)>0。那么 $$P(B_j|A)={P(A|B_j)P(B_j)\over\sum_{i=1}^nP(A|B_i)P(B_i)}$$

4 随机变量

随机变量(random variable)的本质是一个函数，是从样本空间的子集到实数的映射，将事件转换成一个数值。根据样本空间中的元素不同(即不同的实验结果)，随机变量的值也将随机产生。可以说，随机变量是“数值化”的实验结果。

离散随机变量

某个数字来代表样本空间的某个元素，这个数字并不是概率值。如何对样本空间的元素数值化是根据现实需求的。

P(X=x) 表示了随机变量在不同取值下的概率，称为概率质量函数(PMF, probability mass function)。

累积分布函数

我们可以用累积分布函数(CDF, cumulative distribution function)来表示随机变量的概率分布状况。在累积分布函数，我们列出的，总是随机变量X，在小于x的这个区间的概率和。当x增大时，X < x包含的结果增加，概率和也相应增加。当x为正无穷时，实际上是所有情况的概率和，那么累积分布函数为1。

$$F(x)=P(X≤x),−∞<x<∞$$

连续随机变量

随机变量还可以是连续取值，这样的随机变量称为连续随机变量(continuous random variable)。比如，一个随机变量，可以随机的取0到1的任意数值。如时间、温度...

概率密度函数(PDF，probability density function)。粗糙的讲，我们在某个点附近取一个“无穷小”段，该小段的区间长度为dx，而这个“无穷小”段对应的概率为dF，那么该点的概率密度为dF/dx。概率密度函数可以代替累积分布函数，来表示一个连续随机变量的概率分布:

$$f(x)=dF(x)\over dx$$ 即密度函数是累积分布函数的微分 $$F(x)=∫^x_{−∞}f(u)du$$ 即累积分布函数是密度函数从负无穷到x的积分。有 $$∫_{−∞}^{+∞}f(u)du=1$$

5 离散分布

伯努利分布

伯努利分布(Bernoulli distribution)是很简单的离散分布。在伯努利分布下，随机变量只有两个可能的取值: 1和0。随机变量取值1的概率为p。相应的，随机变量取值0的概率为1-p。

二项分布

进行n次独立测试，每次测试成功的概率为p(相应的，失败的概率为1-p)。这n次测试中的“成功次数”是一个随机变量。这个随机变量符合二项分布(binomial distribution)。二项分布可以从计数的角度来理解。n次测试，如果随机变量为k，意味着其中的k次成功，n-k次失败。从n次实验中挑选k个，根据计数原理，共有C(n,k)种可能。其中的每种可能出现的概率为$p^k(1−p)^{n−k}$

$$P(X=k)=C(n,k)p^k(1−p)^{n−k}$$ 在二项分布中n是已知条件

泊松分布

泊松分布(Poisson distribution)是二项分布的一种极限情况，当p→0,n→+∞而np=λ时，二项分布趋近于泊松分布。这意味着我们进行无限多次测试，每次成功概率无穷小，但n和p的乘积是一个有限的数值。

$$P(X=k)={λ^k\over k!}e^{−λ}$$
λ决定了泊松分布的“重心”所在

几何分布

假设我们连续进行独立测试，直到测试成功。每次测试成功的概率为p。那么，到我们成功时，所进行的测试总数是一个随机变量，可以取值1到正无穷。这样一个随机变量符合几何分布(geometric distribution)。随机变量取值为k时，意味前面的k-1次都失败了。因此，我们可以将几何分布表示成:

$$P(X=k)=(1−p)^{k−1}p$$

负二项分布

几何分布实际上是负二项分布(negative geometric distribution)的一种特殊情况。几何分布是进行独立测试，直到出现成功，测试的总数。负二项分布同样是进行独立测试，但直到出现r次成功，测试的总数k。r=1时，负二项分布实际上就是几何分布。在连续的r次测试时，我们只需要保证最后一次测试是成功的，而之前的k-1次中，有r-1次成功。这r-1次成功的测试，可以任意存在于k-1次测试。因此，负二项分布的表达式为:

$$P(X=k)=C(k−1,r−1)p^r(1−p)^{k−r}$$

6 连续分布

指数分布

指数分布(exponential distribution)的密度函数随着取值的变大而指数减小。指数分布的密度函数为:

$$f(x)=λe^{−λx} \text{ if $x\ge 0$}; f(x)=0 \text{ if $x\lt 0$}$$ 累积分布函数为: $$F(x)=1−e^{−λx},x≥0$$

指数分布是无记忆(memoryless)的。我们以原子衰变为例。任意时刻往后，都需要10年的时间，会有一半的原子衰变。已经发生的衰变对后面原子衰变的概率分布无影响

$$P(X>s)=P(X>s+t|X>t),for\ s,t≥0$$

正态分布

正态分布(normal distribution)是最常用到的概率分布。正态分布又被称为高斯分布(Gauss distribution)，因为高斯在1809年使用该分布来预测星体位置。正态分布的发现来自于对误差的估计。早期的物理学家发现，在测量中，测量值的分布很有特点：靠近平均值时，概率大；远离平均值时，概率小。

正态分布的密度函数如下:

$$f(x)={1\over\sqrt{2π}σ}e^{−(x−μ)^2/2σ^2},−∞<x<∞$$ 正态分布有两个参数，μ和σ。我们可以将正态分布表示成N(μ,σ)。当μ=0，σ=1，这样的正态分布被称作标准正态分布(standard normal distribution)。

Gamma分布

Gamma分布在统计推断中具有重要地位。它的密度函数如下:

$$g(t)={λ^α\over Γ(α)}t^{α−1}e^{−λt},t≥0$$ 其中的Gamma函数可以表示为: $$Γ(x)=∫_0^∞u^{x−1}e^{−u}du,x>0$$ 注意到，Gamma分布有两个控制参数α和λ。

7 联合分布

联合分布(joint distribution)描述了多个随机变量的概率分布，是对单一随机变量的自然拓展。联合分布的多个随机变量都定义在同一个样本空间中。

离散随机变量的联合分布

从一个样本空间，可以同时产生多个映射。比如，我们的实验是连续三次投硬币，样本空间为

$$Ω={hhh,hht,hth,thh,htt,tht,tth,ttt}$$ 在同一样本空间上，我们可以定义多个随机变量，比如:

• X: 投掷为正面的总数，可以取值0，1，2，3
• Y: 最后一次出现负面的总数，可以取值0，1
• Z: 将正面记为10，负面记为5，第一次与第三次取值的差，可以有5, -5, 0

这三个随机变量可以看作一个有三个分量的矢量。所以定义在同一样本空间的多随机变量，是一个从样本空间到矢量的映射。

对于X=x,Y=y，我们寻找样本空间中满足这两个取值的所有元素。这些元素构成一个样本空间的子集，该子集的概率就是P(X=x,Y=y)的联合概率。p(x,y)=P(X=x,Y=y)称为联合概率质量函数(joint PMF, joint probability mass function)。联合概率可以看做两个事件同时发生时的概率，事件A为X=x，事件B为Y=y，即P(A∩B)。

连续随机变量的联合分布

在单变量情况下，概率是一个“面积”，是由区间的“长度”和密度函数(一条曲线)围成的。这里的“体积”是二维区间的“面积”和密度函数(一个曲面)围成的。我们可以使用联合概率密度函数(joint PDF, joint probability density function)来表达多随机变量的分布。对于双变量的联合分布来说，它等于无穷小块的概率，除以无穷小块的面积。用微积分的语言来说，就是

$$P(a≤X≤b,c≤Y≤d)=∫_a^b∫_c^df(x,y)dxdy$$ f(x,y)就是描述X和Y的联合分布的联合概率密度函数。联合概率密度函数描述了所有可能取值的情况，因此有 $$∫^{+∞}_{−∞}∫^{+∞}_{−∞}f(x,y)dxdy=1$$

边缘概率

联合分布包含了多个随机变量的分布信息。我们当然可以从联合分布中，提取出任意一个单一随机变量的分布，也就是所谓的边缘分布(marginal distribution)。对于离散随机变量，可以获得边缘概率质量函数(marginal pmf):

$$p_X(x)=∑_{all\ y}p(x,y)$$ $$p_Y(y)=∑_{all\ x}p(x,y)$$ 在求X的单一边缘分布时， 我们累加了相同x值、不同y值时的多个联合概率，从而获得该x值的的总体概率，即边缘概率。
连续随机变量X的边缘密度函数(marginal pdf, marginal probability density function)可以定义为 $$fX(x)=∫^{+∞}_{−∞}f(x,y)dy$$ fX(x)是联合密度函数对Y的积分。通过积分，我们将不同Y取值时的联合概率加在一起，就获得纯粹的单一X的分布状况。

条件分布

与事件的条件概率类似，假设pY(y)≠0，在Y=y的条件下，随机变量X取值为x的概率定义为:

$$p(x|y)={p(x,y)\over p_Y(y)}$$ 即X=x,Y=y同时发生的概率，除以Y取值为y的的概率。

独立随机变量

正如事件之间可以相互独立一样，随机变量之间也可以相互独立。当X独立于Y时，我们可以相像，Y的取值，将不影响X的概率。也就是说

$$p(x|y)=p_X(x)$$ 这意味着，当且仅当 $$p(x,y)=p_X(x)p_Y(y)$$ 时，X和Y相互独立。

8 随机变量的函数

通过事件与随机变量的映射，让事件“数值化”，事件的概率值转移到随机变量上，获得随机变量的概率分布。我们使用随机变量的函数，来定制新的随机变量。随机变量的函数是从旧有的随机变量到一个新随机变量的映射。通过函数的映射功能，原有随机变量对应新的随机变量。通过原有随机变量的概率分布，我们可以获知新随机变量的概率分布。

获得新概率分布的基本方法

如果有函数关系Y=g(X1,X2,...,Xn)，获得Y分布的基本方法是:

1. 通过Y=g(X1,X2,...,Xn)，找到对应{Y≤y}的(x1,x2,...,xn)区间I
2. 在区间I上，积分f(x1,x2,...,xn)，获得P(Y≤y)
3. 通过微分，获得密度函数

单变量函数的通用公式

对于单变量函数来说，如果Y=g(X)，g是一个可微并且单调变化的函数(在该条件，存在反函数$g^{−1}$，使得$X=g^{−1}(Y)$。那么我们可以使用下面的通用公式，来获得Y的分布:

$$f_Y(y)=f_X(g^{−1}(y))⋅{d\over dy}g^{−1}(y)$$

多变量函数的通用公式

如果U=g1(X,Y),V=g2(X,Y)，且存在反变换，使得

$$X=h1(U,V)$$ $$Y=h2(U,V)$$ 那么，我们可以通过如下公式，从X,Y的分布获得U,V的联合分布: $$f_{UV}(u,v)=f_{XY}(h1(u,v),h2(u,v))|J|$$ J表示雅可比变换(Jacobian tranformation)，表示如下 $$J=\begin{vmatrix}{∂x\over ∂u}&{∂x\over ∂v}\\ {∂y \over ∂u}&{∂y\over ∂v}\end{vmatrix} = {∂x\over ∂u}{∂y\over ∂v} - {∂x\over ∂v}{∂y \over ∂u}$$

9 期望

描述量

描述随机变量最完备的方法是写出该随机变量的概率分布。统计学家也设计了这样的投影系统，将全面的概率分布信息量投射到某几个量上，来代表随机变量的主要特征，从而掌握该随机变量的主要“性能”。这样的一些量称为随机变量的描述量(descriptor)。比如期望用于表示分布的中心位置，方差用于表示分布的分散程度等等。这些描述量可以迅速的传递其概率分布的一些主要信息，允许我们在深入研究之前，先对其特征有一个大概了解。

期望

期望(expectation)是概率分布的一个经典描述量，它有很深的现实根源。在生活中，我们往往对未知事件有一个预期，也就是我们的期望。

在概率论中，我们更加定量的对未知结果进行预估。根据概率分布，我们以概率值为权重，加权平均所有可能的取值，来获得了该随机变量的期望(expectation):

$$E(x)=∑_ix_ip(x_i)$$ 期望常用字母μ表示 (μ同样是高斯分布的一个参数)

基于相似的道理，可以用下面的积分公式，计算连续随机变量的期望：

$$E(X)=∫^{+∞}_{−∞}xf(x)dx$$
正态分布的期望 $$E(X)={1\over σ\sqrt{2π}}∫^{+∞}_{−∞}xe^{−(x−μ)^2\over2σ^2}dx=μ$$ 分布的参数μμ就是正态分布的期望

指数分布的期望

$$E(x)=1/λ$$

期望的性质

性质1

如果Y=g(X)，那么当X为离散随即变量，且∑|g(x)|p(x)<∞ (该条件保证下面的累加为有限值) $$E(Y)=∑_xg(x)p(x)$$ 当X为连续随机变量，且$∫|g(x)|f(x)dx<∞$(该条件保证下面的积分为有限值) $$E(Y)=∫^{+∞}_{−∞}g(x)f(x)dx$$

性质2

Y=g(X1,X2,...,Xn)。如果Xi是离散的，且有分布p(x1,...,xn)，那么当$∑_{x1,...,xn}|g(x1,...,xn)|p(x1,...,xn)<∞$时，有 $$E(Y)=∑_{x_1,...,x_n}g(x_1,...,x_n)p(x_1,...,x_n)$$ 如果Xi是连续的，且有分布f(x1,...,xn)，那么当$∫∫...∫|g(x1,...,xn)|f(x1,...,xn)dx<∞$时，有 $$E(Y)=∫∫...∫g(x_1,...,x_n)f(x_1,...,x_n)dx$$

性质3

如果X和Y是独立随机变量，而g和h是两个函数，如果E[g(X)],E[h(Y)]存在，那么有 $$E[g(X)h(Y)]=E[g(X)]E[h(Y)]$$ 当gh为直接返回函数时，可容易推出如果X和Y独立，那么 $$E(XY)=E(X)E(Y)$$

性质4

如果$Y=a+∑^n_{i=1}b_iX_i$，而Xi的期望为E(Xi)，那么 $$E(Y)=a+∑_{i=1}^nb_iE(X_i)$$ 这说明，期望是一个线性运算。随机变量线性组合的期望，等于期望的线性组合。

条件期望

条件期望将期望用于条件概率。我们已经知道，条件概率是事件B条件下，A的概率，即P(A|B)。条件概率只不过是在一个缩小了的样本空间B上，重新计算A的概率。条件概率的A与B可以是随机变量，比如P(X|Y=y)，即“随机变量Y等于y”是条件，在该条件下，随机变量X的随机分布。(在连续随机变量的情况下，我们使用条件密度函数f(x|Y=y)来描述条件分布)

对于一个已知的分布，我们可以求得条件分布的期望。对于离散随机变量:

$$E(X|Y=y)=∑_ix_ip(x_i|Y=y)$$ 其中，xi该离散随机变量的可能取值。也就是，在一个新的样本空间(Y = y)上，随机变量X的期望值。对于连续随机变量，其条件期望为: $$E(X|Y=y)=∫^{+∞}_{−∞}xf(x|Y=y)dx$$

一个随机变量的期望为一个数值。但一个条件分布的期望，比如E(X|Y=y)，会随着随机变量Y的变化而变化。所以，条件期望是随机变量Y的函数。根据随机变量的函数的概念，E(X|Y=y)可以看作一个新的随机变量。我们可以进一步得到这一新的随机变量的期望E(E(X|Y))。

10 方差与标准差

方差就是分布的离散程度。方差越大，说明随机变量取值越离散。

方差

对于一个随机变量X来说，它的方差为:

$$Var(X)=E[(X−μ)^2]$$ 其中，μ表示X的期望值，即μ=E(X)。代入期望的数学表达形式。比如连续随机变量： $$Var(X)=E[(X−μ)^2]=∫^{+∞}_{−∞}(x−μ)^2f(x)dx$$ 由于取值是随机的，不同取值的概率不同，我们根据概率对该平方进行加权平均，也就获得整体的离散程度——方差。

方差的平方根称为标准差(standard deviation, 简写std)。我们常用σ表示标准差

$$σ=\sqrt{Var(X)}$$ 标准差也表示分布的离散程度。

正态分布的方差

可以算出正态分布 $$E(X)={1\over σ\sqrt{2π}}∫^{+∞}_{−∞}xe^{−(x−μ)^2/2σ^2}dx$$ 方差为 $$Var(X)=σ^2$$
正态分布的标准差正等于正态分布中的参数σ。这正是我们使用字母σ来表示标准差的原因！

指数分布的方差

指数分布的方差为 $$Var(X)={1\over λ^2}$$

Chebyshev不等式

标准差(和方差)表示分布的离散程度。标准差越大，随机变量取值偏离平均值的可能性越大。可以计算一个随机变量与期望偏离超过某个量的可能性。比如偏离超过2个标准差的可能性。即

$$P(|X−μ|>2σ)$$

无论μ和σ如何取值，对于正态分布来说，偏离期望超过两个标准差的概率都相同，约等于0.0455 (可以根据正态分布的表达式计算).

Chebyshev不等式让我们摆脱了对分布类型的依赖。对于任意随机变量X，如果它的期望为μ，方差为σ2，那么对于任意t>0，

$$P(|X−μ|>t)≤{σ^2\over t}$$ 无论X是什么分布，上述不等式成立。我们让t=2σ，那么 $$P(|X−μ|>2σ)≤0.25$$

11 协方差与相关系数

协方差

协方差(covariance)表达了两个随机变量的协同变化关系。

协方差的定义

如果X和Y是联合分布的随机变量，且分别有期望μX，μY，那么X和Y的协方差为 $$Cov(X,Y)=E[(X−μ_X)(Y−μ_Y)]$$

根据期望的性质，我们可以改写协方差的表达形式:

$$Cov(X,Y)=E(XY−Xμ_Y−Yμ_X+μ_Xμ_Y)=E(XY)−E(X)μ_Y−E(Y)μ_X+μ_Xμ_Y=E(XY)−E(X)E(Y)$$

当X和Y独立时，有E(XY)=E(X)E(Y)，Cov(X,Y)=0。(注意，Cov(X,Y)=0并不意味着X和Y独立)

相关系数

正的协方差表达了正相关性，负的协方差表达了负相关性。对于同样的两个随机变量来说，计算出的协方差越大，相关性越强。

相关系数(correlation coefficient)。相关系数是“归一化”的协方差。它的定义如下:

$$ρ={Cov(X,Y)\over \sqrt{Var(X)Var(Y)}}$$

双变量正态分布

双变量正态分布是一种常见的联合分布。它描述了两个随机变量X1和X2的概率分布。概率密度的表达式如下：

$$f(x1,x2)={1\over 2πσ_1σ_2\sqrt{1−ρ^2}}\exp(−{z\over 2(1−ρ^2)})$$ 其中 $$z={(x_1−μ_1)^2\overσ_1^2}−{2ρ(x_1−μ_1)(x_2−μ_2)\over σ_1σ_2}+{(x_2−μ_2)^2\over σ^2_2}$$ X1和X2的边缘密度分别为两个正态分布，即正态分布N(μ1,σ1), N(μ2,σ2)。ρ 正是双变量正态分布中，两个变量的相关系数

12 矩与矩生成函数

斜度

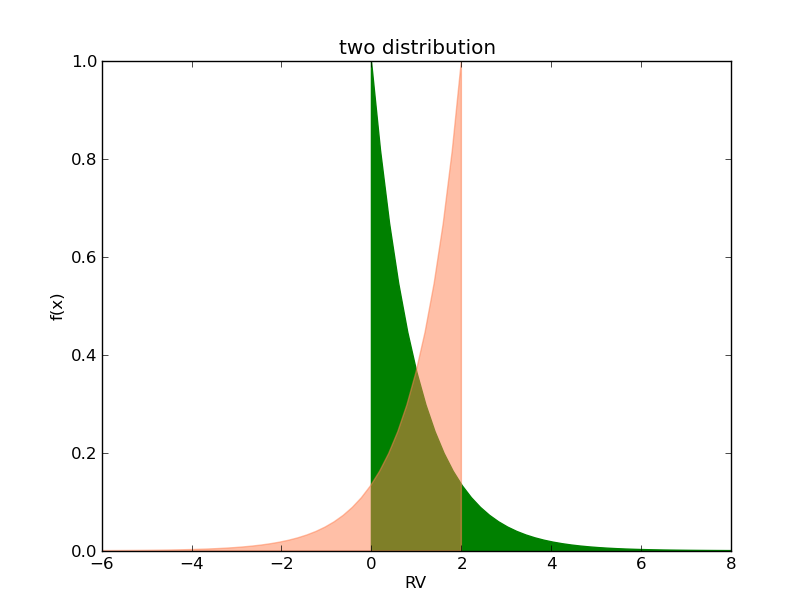
如该图中，两个期望和方差均一样。引入一个新的描述量，斜度(skewness)

$$Skew(X)=E[(X−μ)^3]$$ 第一条曲线向左偏斜，斜度分别为2。另一条曲线的斜度为-2。

矩

方差和斜度都可以归为“矩”(moment)的一族描述量。类似于方差和斜度这样的，它们都是(X−μ)乘方的期望，称为中心矩(central moment)。

$$E[(x−μ)^k]$$ 称为k阶中心矩，表示为μk，其中k = 2, 3, 4, ...

原点矩(moment about the origin)，是X乘方的期望。

$$E[X^k]$$ 称为k阶原点矩，表示为$μ′_k$，其中k = 1, 2, 3, ...
期望是一阶原点矩:$E(X)=E(X^1)$

矩生成函数

幂级数(power series)。幂级数是不同阶数的乘方(比如$1,x,x^2,x^3...)$的加权总和：

$$∑_{i=1}^{+∞}a_ix_i$$ $a_i$是一个常数。
将解析函数分解为幂级数的过程，就是泰勒分解(Taylor）

将幂级数的x看作随机变量X，并求期望。根据期望可以线性相加的特征，有:

$$E(f(X))=a_0+a_1E(X)+a_2E(X^2)+a_3E(X^3)+...$$ 我们可以通过矩，来计算f(X)的期望。

另一方面，我们可否通过解析函数来获得矩呢？我们观察下面一个指数函数，写成幂级数的形式：

$$e^{tx}=1+tx+(tx)^2/2!+(tx)^3/3!+(tx)^4/4!...$$ 我们再次将x看作随机变量X，并对两侧求期望，即 $$E(e^{tX})=1+tE(X)+t^2E(X^2)/2!+t^3E(X^3)/3!+t^4E(X^4)/4!...$$ 即使随机变量的分布确定，$E(e^{tX})$的值还是会随t的变化而变化，因此这是一个关于t的函数。我们将它记为M(t)，这就是矩生成函数(moment generating function)。对M(t)的级数形式求导，并让t等于0，可以让高阶的t的乘方消失，只留下E(X)，即 $$M′(0)=E(X)$$ 即一阶矩。如果继续求高阶导，并让t等于0，可以获得高阶的矩。 $$M^{(r)}(0)=E(X^r)$$ 有趣的是，多次求导系数正好等于幂级数系数中的阶乘，所以可以得到上面优美的形式。我们通过幂级数的形式证明了，对矩生成函数求导，可以获得各阶的矩。相对于积分，求导是一个容易进行的操作。

矩生成函数的性质

矩生成函数的另一面，是它的指数函数的解析形式。即

$$M(t)=E[e^{tX}]=∫^∞_{−∞}e^{tx}f(x)dx$$ 在我们获知了f(x)的具体形式之后，我们可以利用该积分获得矩生成函数，然后求得各阶的矩。

性质1

如果X的矩生成函数为$M_X(t)$，且$Y=aX+b$，且$Y=aX+b$，那么 $$M_Y(t)=e^{at}M_X(bt)$$
(将Y写成指数形式的期望，很容易证明该结论)

性质2

如果X和Y是独立随机变量，分别有矩生成函数MX,MY。那么对于随机变量Z=X+Y，有 $$M_Z(t)=M_X(t)M_Y(t)$$ (基于独立随机变量乘积的期望，等于随机变量期望的乘积)

13 中心极限定律

中心极限定律(central limit theorem)

随机变量X1,X2,...,Xn是相互独立的随机变量，并有相同的分布(IID, independent and identically distributed)。分布的期望为μ，方差为σ^2，μ,σ都为有限值，且σ≠0。这些随机变量的均值为$\bar X={1\over n}∑^n_{i=1}X_i$。让$ζ_n={\bar X−μ\over σ/\sqrt{n}}$，那么

$$\lim_{n→∞}P(ζ_n≤z)=Φ(z)$$ 其中Φ(z)是标准正态分布的分布函数。

简单来说，我们寻找n个IID随机变量的均值$\bar X$。当n趋进无穷时，这个均值(一个新的随机变量)趋近一个正态分布。

证明

假设Xi−μ的矩生成函数为M(t)。因此，$M′(t)=μ,M^{(2)}(t)=σ^2$。
当n趋近无穷时，$t/(σ\sqrt{n})$趋近0。M(t)可以展开为:

$$M(t)=1+{1\over 2}σ^2t^2+o(t^2)$$ o(t^2)表示比t^2更高阶的t的乘方。根据矩生成函数的性质，ζn的矩生成函数写为 $$M_{ζ_n}=[M({t\over σ\sqrt{n}})]^n=(1+{t^2\over2n}+o(t^2/n))^n$$ o(t2/n)表示，当n趋于无穷时，早于t2/nt2/n消失的项。
当n趋近于无穷时，上面的表达式趋近： $$M_{ζ_n}(t)→e^{t^2/2}$$ 这正是标准正态分布的矩生成函数。因此ZnZn的分布趋近于标准正态分布。