@spiritnotes
2016-03-08T10:22:17.000000Z
字数 8996
阅读 3050
Matplotlib Tutorial -- 学习笔记
Python
原文: http://reverland.org/python/2012/09/07/matplotlib-tutorial
简单绘图
from pylab import *figure(figsize=(8,6), dpi=80)subplot(1,1,1)plot(X, C, color="blue", linewidth=1.0, linestyle="-")plot(X, S, color="green", linewidth=1.0, linestyle="-")xlim(-4.0,4.0)xticks(np.linspace(-4,4,9,endpoint=True))ylim(-1.0,1.0)yticks(np.linspace(-1,1,5,endpoint=True))
线条变宽
figure(figsize=(10,6), dpi=80) # 图像更大plot(X, C, color="blue", linewidth=2.5, linestyle="-")plot(X, S, color="green", linewidth=2.5, linestyle="-") #像素点
设置边界
xlim(X.min()*1.1, X.max()*1.1)ylim(C.min()*1.1, C.max()*1.1)
设置刻度
xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi])yticks([-1, 0, +1])
设置刻度标签
xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi],[r'$-\pi$', r'$-\pi/2$', r'$0$', r'$+\pi/2$', r'$+\pi$'])yticks([-1, 0, +1],[r'$-1$', r'$0$', r'$+1$'])
移动轴线(spine)
轴线(spines)是连接刻度标志和标示数据区域边界的线。它们现在可以被放置在任意地方,它们在子图的边缘。我们将改变这点,因为我们想让它们位于中间。因为一共有四个轴线(上/下/左/右)。我们将通过将它们的颜色设置成None,舍弃位于顶部和右部轴线。然后我们把底部和左部的轴线移动到数据空间坐标中的零点。
ax = gca()ax.spines['right'].set_color('none')ax.spines['top'].set_color('none')ax.xaxis.set_ticks_position('bottom')ax.spines['bottom'].set_position(('data',0))ax.yaxis.set_ticks_position('left')ax.spines['left'].set_position(('data',0))
添加图例
plot(X, C, color="blue", linewidth=2.5, linestyle="-", label="cosine")plot(X, S, color="red", linewidth=2.5, linestyle="-", label="sine")legend(loc='upper left')
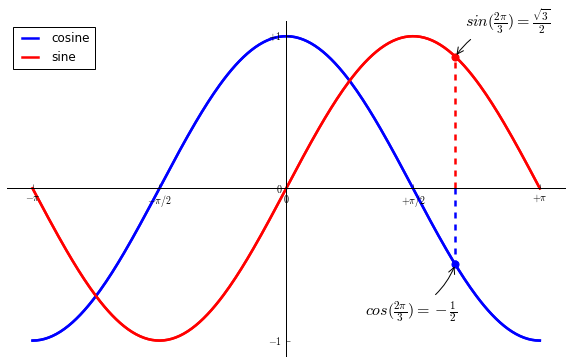
注解某些点
t = 2*np.pi/3plot([t,t],[0,np.cos(t)], color ='blue', linewidth=2.5, linestyle="--")scatter([t,],[np.cos(t),], 50, color ='blue')annotate(r'$sin(\frac{2\pi}{3})=\frac{\sqrt{3}}{2}$',xy=(t, np.sin(t)), xycoords='data',xytext=(+10, +30), textcoords='offset points', fontsize=16,arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))plot([t,t],[0,np.sin(t)], color ='red', linewidth=2.5, linestyle="--")scatter([t,],[np.sin(t),], 50, color ='red')annotate(r'$cos(\frac{2\pi}{3})=-\frac{1}{2}$',xy=(t, np.cos(t)), xycoords='data',xytext=(-90, -50), textcoords='offset points', fontsize=16,arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
魔鬼在于细节
调整标签
for label in ax.get_xticklabels() + ax.get_yticklabels():label.set_fontsize(16)label.set_bbox(dict(facecolor='white', edgecolor='None', alpha=0.65 ))
图像、子区、子图、刻度
一个图像(figure)意味着用户界面的整个窗口。在一个图像中可以有些子区(subplot)。subplot将绘图放置在常规的网格位置上而axes允许更自由的放置。它们都非常有用,取决于你的意图。我们已经隐式地使用了figure和subplot。当我们调用plot时,matplotlib调用gca来获取当前axes反过来调用gcf()获取当前图像(figure)。如果没有当前图像(figure),它调用figure()创建一个,严格地说,是创建一个subplot(111)。
图像(Figure)
| 参数 | 默认 | 描述 |
|---|---|---|
| num | 1 | 图像编号 |
| figsize | figure.figsize | 图像大小(宽度,高度)(英寸) |
| dpi | figure.dpi | 每英寸分辨率 |
| facecolor | figure.facecolor | 背景色 |
| edgecolor | figure.edgecolor | 绘图背景边沿色 |
| frameon | True | 绘制框架与否 |
子区(subplots)
subplot(x,y,1)
你可以通过subplot在正常网格中布置图像。你需要指定行数和列数和区域的编号。注意gridspec命令是个更强大的选择。
子图(axes)
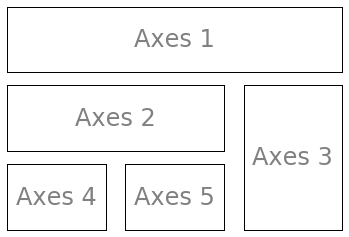
子图和子区(subplot)非常相似,但是允许把图片放置到图像(figure)中的任何地方。所以如果我们想要在一个大图片中嵌套一个小点的图片,我们通过子图(axes)来完成它。
import matplotlib.gridspec as gridspecG = gridspec.GridSpec(3, 3)axes_1 = subplot(G[0, :])xticks([]), yticks([])text(0.5,0.5, 'Axes 1',ha='center',va='center',size=24,alpha=.5)axes_2 = subplot(G[1,:-1])xticks([]), yticks([])text(0.5,0.5, 'Axes 2',ha='center',va='center',size=24,alpha=.5)axes_3 = subplot(G[1:, -1])xticks([]), yticks([])text(0.5,0.5, 'Axes 3',ha='center',va='center',size=24,alpha=.5)axes_4 = subplot(G[-1,0])xticks([]), yticks([])text(0.5,0.5, 'Axes 4',ha='center',va='center',size=24,alpha=.5)axes_5 = subplot(G[-1,-2])xticks([]), yticks([])text(0.5,0.5, 'Axes 5',ha='center',va='center',size=24,alpha=.5)
axes([0.1,0.1,.8,.8])xticks([]), yticks([])text(0.6,0.6, 'axes([0.1,0.1,.8,.8])',ha='center',va='center',size=20,alpha=.5)axes([0.2,0.2,.3,.3])xticks([]), yticks([])text(0.5,0.5, 'axes([0.2,0.2,.3,.3])',ha='center',va='center',size=16,alpha=.5)

axes([0.1,0.1,.5,.5])xticks([]), yticks([])text(0.1,0.1, 'axes([0.1,0.1,.8,.8])',ha='left',va='center',size=16,alpha=.5)axes([0.2,0.2,.5,.5])xticks([]), yticks([])text(0.1,0.1, 'axes([0.2,0.2,.5,.5])',ha='left',va='center',size=16,alpha=.5)axes([0.3,0.3,.5,.5])xticks([]), yticks([])text(0.1,0.1, 'axes([0.3,0.3,.5,.5])',ha='left',va='center',size=16,alpha=.5)axes([0.4,0.4,.5,.5])xticks([]), yticks([])text(0.1,0.1, 'axes([0.4,0.4,.5,.5])',ha='left',va='center',size=16,alpha=.5)

刻度(ticks)
良好格式化的刻度是准备发表的图片中的重要部分。Matplotlib为刻度提供完全可配置的系统。刻度定位器指定刻度出现的位置,刻度格式器让刻度看起来如你所愿。主刻度和次要刻度可以分别放置和格式化,每个默认主刻度并不显示,也就是,它们只有一个空列表,因为它们作为空定位器(NullLocator)(参见下面)
刻度定位器(Tick Locator)
| Class | Description |
|---|---|
| NullLocator | 没有刻度 |
| IndexLocator | 每到一个基数的倍数点放置一个刻度 |
| FixedLocator | 刻度位置是固定的 |
| LinearLocator | 决定刻度位置 |
| MultipleLocator | 在每个基于基数倍数的整数点放置刻度 |
| AutoLocator | 在不错的位置选择不超过n个间隔 |
| LogLocator | 以log坐标决定刻度位置 |
其他种类绘图
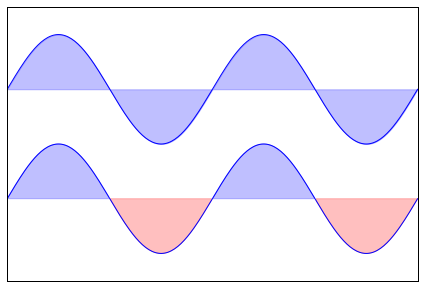
常规绘图
n = 256X = np.linspace(-np.pi,np.pi,n,endpoint=True)Y = np.sin(2*X)plt.axes([0.025,0.025,0.95,0.95])plt.plot (X, Y+1, color='blue', alpha=1.00)plt.fill_between(X, 1, Y+1, color='blue', alpha=.25)plt.plot (X, Y-1, color='blue', alpha=1.00)plt.fill_between(X, -1, Y-1, (Y-1) > -1, color='blue', alpha=.25)plt.fill_between(X, -1, Y-1, (Y-1) < -1, color='red', alpha=.25)plt.xlim(-np.pi,np.pi), plt.xticks([])plt.ylim(-2.5,2.5), plt.yticks([])
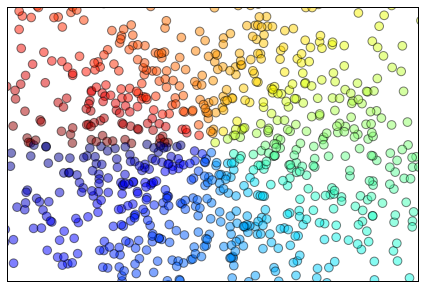
散点图(scatter plots)
n = 1024X = np.random.normal(0,1,n)Y = np.random.normal(0,1,n)T = np.arctan2(Y,X)plt.axes([0.025,0.025,0.95,0.95])plt.scatter(X,Y, s=75, c=T, alpha=.5)plt.xlim(-1.5,1.5), plt.xticks([])plt.ylim(-1.5,1.5), plt.yticks([])
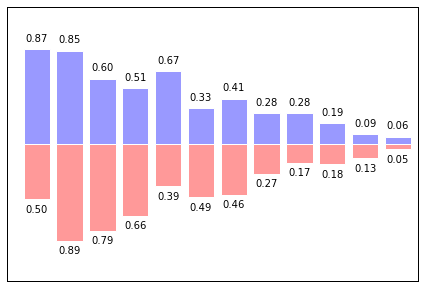
条形图(bar plots)
n = 12X = np.arange(n)Y1 = (1-X/float(n)) * np.random.uniform(0.5,1.0,n)Y2 = (1-X/float(n)) * np.random.uniform(0.5,1.0,n)plt.axes([0.025,0.025,0.95,0.95])plt.bar(X, +Y1, facecolor='#9999ff', edgecolor='white')plt.bar(X, -Y2, facecolor='#ff9999', edgecolor='white')for x,y in zip(X,Y1):plt.text(x+0.4, y+0.05, '%.2f' % y, ha='center', va= 'bottom')for x,y in zip(X,Y2):plt.text(x+0.4, -y-0.05, '%.2f' % y, ha='center', va= 'top')plt.xlim(-.5,n), plt.xticks([])plt.ylim(-1.25,+1.25), plt.yticks([])
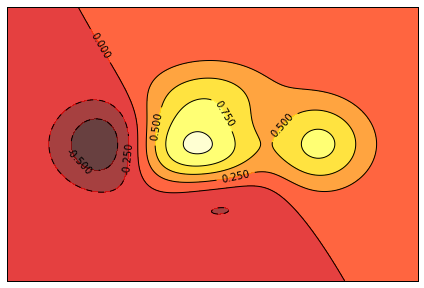
等高线图(contour plots)
n = 256x = np.linspace(-3,3,n)y = np.linspace(-3,3,n)X,Y = np.meshgrid(x,y)def f(x,y):return (1-x/2+x**5+y**3)*np.exp(-x**2-y**2)plt.axes([0.025,0.025,0.95,0.95])plt.contourf(X, Y, f(X,Y), 8, alpha=.75, cmap=plt.cm.hot)C = plt.contour(X, Y, f(X,Y), 8, colors='black', linewidth=.5)plt.clabel(C, inline=1, fontsize=10)plt.xticks([]), plt.yticks([])
Imshow
def f(x,y):return (1-x/2+x**5+y**3)*np.exp(-x**2-y**2)n = 10x = np.linspace(-3,3,3.5*n)y = np.linspace(-3,3,3.0*n)X,Y = np.meshgrid(x,y)Z = f(X,Y)plt.axes([0.025,0.025,0.95,0.95])plt.imshow(Z,interpolation='nearest', cmap='bone', origin='lower')plt.colorbar(shrink=.92)plt.xticks([]), plt.yticks([])

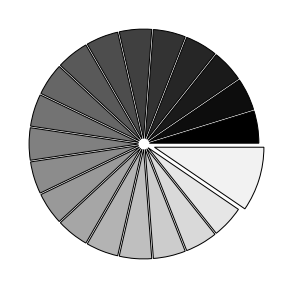
饼图(Pie charts)
n = 20Z = np.ones(n)Z[-1] *= 2plt.axes([0.025,0.025,0.95,0.95])plt.pie(Z, explode=Z*.05, colors = ['%f' % (i/float(n)) for i in range(n)])plt.gca().set_aspect('equal')plt.xticks([]), plt.yticks([])
矢量图(quiver plots)
n = 8X,Y = np.mgrid[0:n,0:n]T = np.arctan2(Y-n/2.0, X-n/2.0)R = 10+np.sqrt((Y-n/2.0)**2+(X-n/2.0)**2)U,V = R*np.cos(T), R*np.sin(T)plt.axes([0.025,0.025,0.95,0.95])plt.quiver(X,Y,U,V,R, alpha=.5)plt.quiver(X,Y,U,V, edgecolor='k', facecolor='None', linewidth=.5)plt.xlim(-1,n), plt.xticks([])plt.ylim(-1,n), plt.yticks([])

网格(grids)
ax = plt.axes([0.025,0.025,0.95,0.95])ax.set_xlim(0,4)ax.set_ylim(0,3)ax.xaxis.set_major_locator(plt.MultipleLocator(1.0))ax.xaxis.set_minor_locator(plt.MultipleLocator(0.1))ax.yaxis.set_major_locator(plt.MultipleLocator(1.0))ax.yaxis.set_minor_locator(plt.MultipleLocator(0.1))ax.grid(which='major', axis='x', linewidth=0.75, linestyle='-', color='0.75')ax.grid(which='minor', axis='x', linewidth=0.25, linestyle='-', color='0.75')ax.grid(which='major', axis='y', linewidth=0.75, linestyle='-', color='0.75')ax.grid(which='minor', axis='y', linewidth=0.25, linestyle='-', color='0.75')ax.set_xticklabels([])ax.set_yticklabels([])
多图绘制
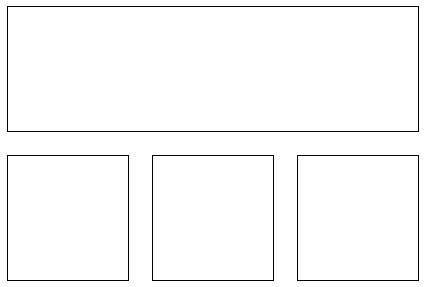
fig = plt.figure()fig.subplots_adjust(bottom=0.025, left=0.025, top = 0.975, right=0.975)plt.subplot(2,1,1)plt.xticks([]), plt.yticks([])plt.subplot(2,3,4)plt.xticks([]), plt.yticks([])plt.subplot(2,3,5)plt.xticks([]), plt.yticks([])plt.subplot(2,3,6)plt.xticks([]), plt.yticks([])
极轴图
ax = plt.axes([0.025,0.025,0.95,0.95], polar=True)N = 20theta = np.arange(0.0, 2*np.pi, 2*np.pi/N)radii = 10*np.random.rand(N)width = np.pi/4*np.random.rand(N)bars = plt.bar(theta, radii, width=width, bottom=0.0)for r,bar in zip(radii, bars):bar.set_facecolor( plt.cm.jet(r/10.))bar.set_alpha(0.5)ax.set_xticklabels([])ax.set_yticklabels([])
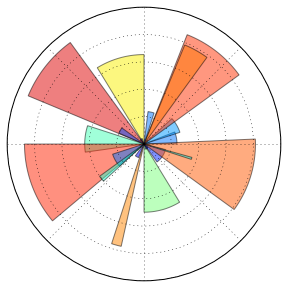
polar=True
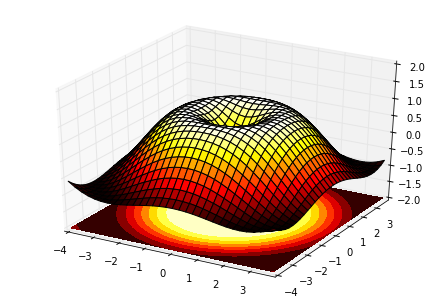
三维绘图
from mpl_toolkits.mplot3d import Axes3Dfig = plt.figure()ax = Axes3D(fig)X = np.arange(-4, 4, 0.25)Y = np.arange(-4, 4, 0.25)X, Y = np.meshgrid(X, Y)R = np.sqrt(X**2 + Y**2)Z = np.sin(R)ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=plt.cm.hot)ax.contourf(X, Y, Z, zdir='z', offset=-2, cmap=plt.cm.hot)ax.set_zlim(-2,2)
绘制文本
eqs = []eqs.append((r"$W^{3\beta}_{\delta_1 \rho_1 \sigma_2} = U^{3\beta}_{\delta_1 \rho_1} + \frac{1}{8 \pi 2} \int^{\alpha_2}_{\alpha_2} d \alpha^\prime_2 \left[\frac{ U^{2\beta}_{\delta_1 \rho_1} - \alpha^\prime_2U^{1\beta}_{\rho_1 \sigma_2} }{U^{0\beta}_{\rho_1 \sigma_2}}\right]$"))eqs.append((r"$\frac{d\rho}{d t} + \rho \vec{v}\cdot\nabla\vec{v} = -\nabla p + \mu\nabla^2 \vec{v} + \rho \vec{g}$"))eqs.append((r"$\int_{-\infty}^\infty e^{-x^2}dx=\sqrt{\pi}$"))eqs.append((r"$E = mc^2 = \sqrt{{m_0}^2c^4 + p^2c^2}$"))eqs.append((r"$F_G = G\frac{m_1m_2}{r^2}$"))plt.axes([0.025,0.025,0.95,0.95])for i in range(24):index = np.random.randint(0,len(eqs))eq = eqs[index]size = np.random.uniform(12,32)x,y = np.random.uniform(0,1,2)alpha = np.random.uniform(0.25,.75)plt.text(x, y, eq, ha='center', va='center', color="#11557c", alpha=alpha,transform=plt.gca().transAxes, fontsize=size, clip_on=True)plt.xticks([]), plt.yticks([])

