The Comparison of Calibration Method of Binocular Stereo Vision System

文献阅读

---

3rd International Conference on Material, Mechanical and Manufacturing Engineering (IC3ME 2015) © 2015. The authors - Published by Atlantis Press

Ke Zhang *, Zhao Gao

双目立体视觉系统中摄像机标定方法的比较

摘要

本文首先给出建立了双目立体视觉实验系统的方法，然后分别使用遗传算法和BP(反向传播)神经网络对立体视觉系统进行摄像机标定。在使用遗传算法的方法中，提出了参数搜索区间自适应调整的编码规则，有效实现了双目立体视觉的高维和非线性系统的摄像机标定；在BP神经网络的方法中，......构建了双目立体视觉系统的隐式校准模型，避免了由于数学模型的缺陷而引起的误差。这两种方法各有优点，分别适合不同的情况。(好像没具体说各自是什么情况？)

介绍

上世纪60年代中期的省理工学院的 Roberts，首创利用提取数字图像中的几何形状信息与3D场景建立联系，标志着立体视觉技术的诞生。之后的研究还进一步分析图形中的阴影，纹理和运动和成像几何等信息。到了上世纪80年代，Marr$[1]$首创视觉计算理论框架，其研究工作形成了从图像采集到3D场景视觉表面重建的完整系统，使立体视觉成为了计算机视觉的重要分支之一。经过几十年的发展，目前立体视觉已经得到了多个行业的广泛应用$[2,3]$。

立体视觉模拟人类视觉的机制，使用双目提示来感知周围的场景，并通过感应设备理解和识别3D信息。 在实际应用中，使用两台摄像机从不同角度拍摄同一物体，然后根据三角测量法来重建三维空间中的物体。

在双目立体视觉系统中，两台相机之间的几何关系将直接影响到它们的公共视野和图像匹配的搜索范围。 因此，需要对整个系统的结构进行分析和选择，依此来构建硬件系统。（摆放摄像机？）

摄像机标定是立体视觉中的难点，实际应用中，因为相机的畸变和设备安装的问题，导致理想的线性模型无法表达摄像机的成像几何关系。诸多非线性因素导致物体和成像之间的关系变得复杂，甚至无法用一个确切的数学模型来进行描述。唯一的方法是，在达到一定精度的前提下对模型进行近似模拟。

进行立体视觉系统中的摄像机标定主要有 2 种方法：一种是用非线性数学模型来近似表示3D 空间点 和两幅图像中对应的 图像点 之间的几何位置关系，摄像机标定的工作就是计算出该数学模型中的参数；另外一种是使用人工神经网络，这种方式不需要建立摄像机的数学模型，而是依靠人工神经网络的非线性拟合能力来构建2D图像坐标系和3D空间坐标系之间的映射关系。

建立双目视觉系统

双目视觉系统有 3 种结构，即：平行光轴结构，公共光轴结构和交叉光轴结构。

在平行光轴结构中$[4]$，两个摄像机的焦距和其他内部参数都与2个光轴（分别垂直于2个摄像机的成像平面）重合，两个摄像机的纵轴互相平行，因此两个摄像机可以通过水平移动彼此重合。这种结构在建立各种几何匹配关系的时候非常方便，但实际安装摄像机的时候很难达成这个条件。此外，为了让两个摄像机在测量物体可见表明的同时观测到平行光轴（不知道这么翻译对不对），必须把两个摄像机安装的很近，这样就造成了两个成像平面之间的投影差异变得很小，进而影响了测量精度。

在公共光轴结构中$[5]$，前后排列的两个摄像机的光轴重合，极平面由空间点和两个摄像机的光心与前后排列的图像平面的交点组成，交线是共轭的，穿过各自的图像平面中心，并且具有相同的斜率。显然，两条穿过图像中心并具有相同斜率的共轭线为两个图像的匹配带来了很多便利。但是，就如同平行光轴系统一样，公共光轴系统也很难让两个摄像机的光轴共线。同时，为了同时观察场景中的同一部分，前后两个摄像机的距离必须足够大，但如果基线距离太大，两个图像就会形成遮挡，就是说，被测量物体的一些表面区域，可能会出现在一副图像中而不出现在另一幅中，或者甚至两幅中都不会出现。当测量的3D表面的曲率半径较大并且表面变化剧烈时，这种现象会尤为严重。

交叉光轴结构如图1所示，左右两个摄像机的光轴$z_l$和$z_r$以某个角度排列。这种结构中，摄像机的摆放比较容易，并且可以根据被测量物体的特性和系统的需要，灵活的调整距离和斜率方向。这样，可以从结构上避免上述两种结构中存在的视野过小和图像遮挡问题。但是，从图中可以看出，共轭极线$p_l$和$p_r$的分布不利于两个图像的匹配。（Why?）

综合对比了三种结构的特性，本文的双目立体视觉系统选择了交叉光轴结构，这样既可以更容易的安装和调整，又可以实现平滑的图像匹配。该结构在实际应用中也经常被使用。

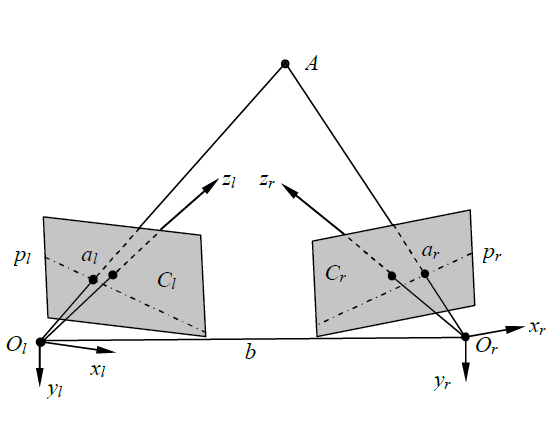
图1 交叉光轴结构

基于遗传算法进行标定

对于构建双目立体视觉系统，由于径向失真因素的影响，双摄像机标定是一个非线性复杂函数优化的问题。处理这个优化问题的传统方法包括牛顿法，梯度下降法和共轭梯度法等。但是，这些方法都需要设置合适的初始参数值，否则，会产生优化过程的收敛性差，或者收敛到局部极值的问题。特别是对于大规模非线性优化问题，寻求全局最优解的难度会随着局部极值的增加而增加。

遗传算法$[6]$是一种解决全局优化问题而产生的一种自适应搜索概率算法。它采用群体搜索技术，通过对当前群进行选择，交叉和突变等操作，来生成新的群。

遗传算法在摄像机标定领域有广泛的应用，但主要集中在单目视觉系统的标定上。Qiang $[7]$采用遗传算法标定摄像机参数的工作中，在收敛性，准确性和鲁棒性上的表现都很好。但是，由于摄像机模型中不包括镜头的失真因素，在3D测量上的准确度很难保证。另外，Roberts $[8]$ 指出，标准的遗传算法可能无法符合参数数量大于10的高维优化空间的精度要求，同时，他的研究结果也表明了，遗传算法的效率会随着优化空间的维度增加而急剧下降。

自适应变量搜索区间调整方法是通过调整两个区间来实现的。有两个与变量有关的区间，大的区间$[A_i^{min}, A_i^{max}]$表示变量的取值范围，值在初始化后不变。小的区间$[a_i^-, a_i^+]$可以在大区间中移动，在移动的过程中长度不变。小区间的目的是为了确保在编码变量时的准确性。通过在整个变量的取值范围内移动小区间来寻找最优解。

用左右两个CCD摄像机对黑白格标定板进行拍摄。共得到126个测试点。经过图像处理和实际的测量步骤，得到相应的126组数据，每一组数据中包括左右2个图像点坐标$(u_l,v_l)$和$(u_r,v_r)$，以及3D空间中的空间点坐标$(X_w,Y_w,Z_w)$。这126组数据分成标定和测试两组，24个点用来标定计算，其他102个点用来在标定后测试3D测量的精度。

将测试点的两个图像点坐标$(u_l,v_l)$和$(u_r,v_r)$传入双目视觉系统的标定测量系统中，经过三维重建后，会得到一组3D空间点坐标$(X'_w,Y'_w,Z'_w)$。然后将其与测试点的实际的3D空间点坐标$(X_w,Y_w,Z_w)$进行比较，测量的平均误差统计在表1中，并与24个标定点的结果进行对比。

	$X_w$方向（mm）	$Y_w$方向（mm）	$Z_w$方向（mm）
标定点	0.37	0.56	1.32
测试点	0.33	0.63	1.27

表1 平均测量误差对比

实验结果表明，虽然双目视觉系统的非线性复杂度和多维优化的解空间很大，但改进的遗传算法在近似最优解方面还是具有比较好的收敛性。

基于BP神经网络进行标定

对于立体视觉系统来说，摄像机标定的终极目标是建立物体点的2D坐标和3D坐标之间的映射关系，从左右两个图像平面的图像点2D坐标直接生成3D空间的空间点坐标。所以，没有必要解出摄像机的所有物理参数，一些物理参数可以整合到一些中间参数中计算，这样，一定程度上简化了计算过程并提高了标定的精度。这种方法叫做隐式标定。与之相对的，通过建立数学模型来求解出摄像机的内部和外部物理参数的方法叫做显示标定$[9]$。

人工神经网络（ANN）的内部机制与隐式标定很相似，两种方法都是通过已知数据建立模型来求解未知数据。基于人工神经网络进行摄像机标定的方法，不需要建立立体视觉系统的数学模型，这样可以避免因为数学模型的缺陷导致的误差，进而避免显示标定的缺陷，提高测量精度。

扩展性和泛化能力是衡量一个神经网络的重要指标，好的泛化能力指不仅要对训练样本集有比较好的匹配，而且还要对新样本有近似正确目标的输出。标准的反向传播算法容易出现局部最小值，收敛过慢和过度训练的问题，这样不仅影响训练结果，延长收敛时间，还会影响泛化能力。正则化方法通过改进标准BP神经网络的训练性能函数来提升泛化能力。

一般来说，反向传播算法的性能函数（就是损失函数吗？）采用均方差函数 $mse$。假设有$N$个训练样本$[X_i,Y_i](i=1,2,...,N)$，网络的权重和阈值是随机的，输入$X_i$，对应输出$\bar{Y_i}$，则该样本的均方差函数如下所示：

$$mse=\frac{1}{N}\sum_{i=1}^N (Y_i-\bar{Y_i})^2--------------(1)$$
而在正则化方法中，性能函数如下所示：
$$E=\gamma \cdot mse+(1-\gamma)\cdot msw-------------(2)$$
其中，$\gamma$ 表示比例因子，而$msw$表示网络中所有权重的均方(平方的平均值)：
$$msw=\frac{1}{M}\sum_{j=1}^M w_j^2------------------(3)$$

正则化方法在训练网络的过程中会自适应的调整 $\gamma$ 的值，让网络的权重值更小，进而最小化误差函数 $E$ 。这相当于自动减小网络的尺寸（意思是不是很多神经元的权重很小，就相当于不参与函数了？）进而减少过度训练的机会，也就相当于达到了提高神经网络泛化能力的目标（过度训练和泛化之间有必然联系吗？过度训练导致过拟合？）。

对于标定板图像，一共有21个标定位置，每个标定位置有216个标定点，这样标定点的总数即为4536个。标定点实际的空间位置，由标定板所处位置和该点在标定板上的位置决定。而每个标定点在左右两个图像平面的图像位置是通过角提取过程得到的，如图2所示。

图2 角提取

数据样本由每个标定点在左右2个图像平面的图像坐标和3D空间坐标组成。所有的4536个标定点分成2组，分别是800个训练样本和3736个测试样本。

BP神经网络的训练结果如表2所示。

平均误差(mm)	最大误差(mm)

$\Delta X$	$\Delta Y$	$\Delta Z$	$\Delta X$	$\Delta Y$	$\Delta Z$
0.0548	0.0529	0.2744	0.2533	0.2467	0.9561

表2 训练误差

测试样本的误差数据如表3所示。

平均误差(mm)	最大误差(mm)

$\Delta X$	$\Delta Y$	$\Delta Z$	$\Delta X$	$\Delta Y$	$\Delta Z$
0.0579	0.0536	0.2972	0.3197	0.2739	1.3578

表3 测试误差

实验结果表明，BP神经网络在训练集和测试集上的精度很接近，这说明BP神经网络在有效的标定3D空间上具有良好的泛化能力。

总结

使用遗传算法标定双摄像机，可以分别求解两个摄像机的内部和外部参数。通过使用自适应编码方法，解决非线性和复杂函数求解的能力得到了加强。人工神经网络可以实现复杂非线性映射的高阶逼近，因而提供了一种实现立体视觉系统摄像机标定的有效方法，该方法不需要考虑镜头失真和环境因素的影响，因而可以避免数学模型的缺陷，提高测量精度。

参考文献

$[1]$ Marr D.Vision.W.H.Freeman and Company, San Francisco. Chinese version: computational theory of vision. G.Z. Yao，L.Liu and Y.J.Wang，Science Press. Beijing, China, 1988, pp. 6-37(In Chinese).
$[2]$ S.Y. You and G.Y. Xu: Journal of Image and Graphics. Vol. 2, No. 1, (1997), pp. 17~24(In Chinese).
$[3]$ Y.D. Jia: Machine Vision. Science Press. Beijing, China, 2000, pp. 1-25(In Chinese).
$[4]$ S.D. Ma and Z.Y. Zhang: Computer Vision-Fundamentals of Computational Theory and Algorithms. Science Press. Beijing, China, 1998, pp. 72-93(In Chinese).
$[5]$ M. Kong and S.M. Wang: Journal of Metrology. Vol. 25, No. 4, (2004), pp. 294~297(In Chinese).
$[6]$ M. Zhou and S.D Sun: Principle and Application of Genetic Algorithm. National Defense Industry Press. Beijing, China, 2002, pp. 4-64(In Chinese).
$[7]$ J. Qiang and Y.M. Zhang: IEEE Transactions on Systems, Man, and Cybernetics－Part A: Systems and Humans. Vol. 31, No. 2, (2001), pp. 120~130.
$[8]$ Roberts M and Naftel A J: Genetic Algorithms in Image Processing and Vision. IEE Colloquium on, 1994: 12/1~12/5
$[9]$ G.Q. Wei and S.D. Ma: IEEE Transactions on Pattern Analysis and Machine Intelligence. Vol. 16, No. 5, (1994), pp. 469~480.