机器人作业2_袁胜_2016M8009073008

作业

---

练习 2_1

公式推导过程

$$\nu = \frac{r\Phi_r}{2} + \frac{r\Phi_l}{2} ----- (1)$$
$$\omega = \frac{r\Phi_r}{2l} - \frac{r\Phi_l}{2l} ----- (2)$$
$$(2) \times l ===>$$
$$l\omega = \frac{r\Phi_r}{2} - \frac{r\Phi_l}{2} ----- (3)$$
$$(1) + (3) ===>$$
$$\Phi_r = \frac{\nu + l\omega}{r} ----- (4)$$
$$(1) - (3) ===>$$
$$\Phi_l = \frac{\nu - l\omega}{r} ----- (5)$$
$\Phi_l$ 即 calculateWheelSpeeds.m 中的 LeftWheelVelocity；而 $\Phi_r$ 即为 RightWheelVelocity.

calculateWheelSpeeds.m 的 TODO 部分程序：

% ----------------------------
% ex_2_1
% In exercise2-assignment.pdf
% v is vu here
% w is omega here
% r is wheelRadius here
% l is halfWheelbase here
% /Phi(l) and /Phi(r) are LeftWheelVelocity and RightWheelVelocity here
% ----------------------------
LeftWheelVelocity = (vu - halfWheelbase * omega) / wheelRadius;
RightWheelVelocity = (vu + halfWheelbase * omega) / wheelRadius;

运行结果：

输出：

Congratulations! All checks successful, your implementation is most likely correct!

图片：

练习 2_2

calculateControlOutput.m 中增加的程序

% exercise2-assignment.pdf 中的 beta
beta = - (lambda + thetag);
beta = normalizeAngle(beta);
...
% ----------------------------
% ex_2_2
% exercise2-assignment.pdf 中的公式 (3) (4)
% ----------------------------
vu = parameters.Krho * rho;% [m/s] 
omega = parameters.Kalpha * alpha + parameters.Kbeta * beta;% [rad/s]

运行结果

起初速度快，接近目标后速度变慢，路径如下：

练习 2_3

calculateControlOutput.m 的 后半部分

% ex_2_3
% 1 正向，-1 反向
direction = 1; 
if parameters.backwardAllowed && parameters.useConstantSpeed;
    % 如果是反向
    if abs(alpha) > pi() / 2
       % 转方向到 backward
       alpha = normalizeAngle(alpha - pi());
       beta = normalizeAngle(beta - pi());
       direction = -1; 
       % 更新 omega
       omega = parameters.Kalpha * alpha + parameters.Kbeta * beta;
    end
    % 根据 vu 的缩放调整 omega
    omega = omega * (parameters.constantSpeed / vu);
    % 常数速度
    vu = direction * parameters.constantSpeed;
end

运行结果

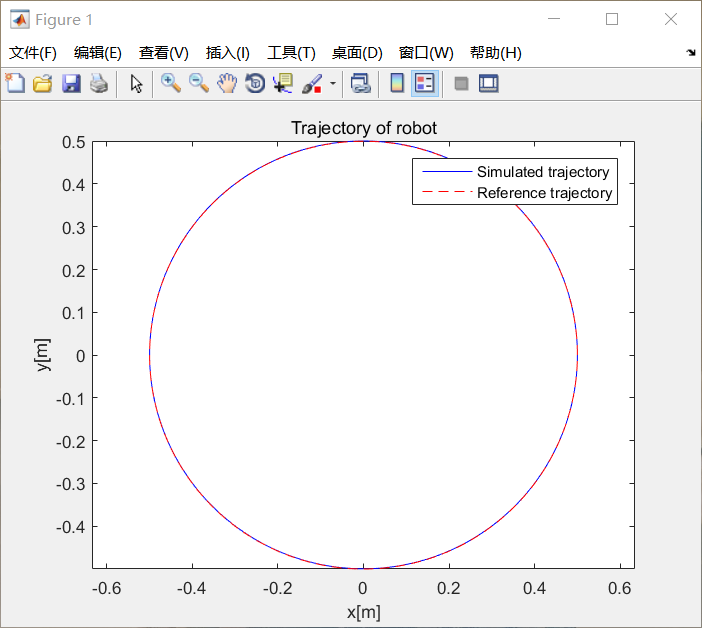
路径与 ex_2_2 一致，匀速接近目标并很快找到目标。路径如下：